东北育才 NOIP模拟赛第1场

　　

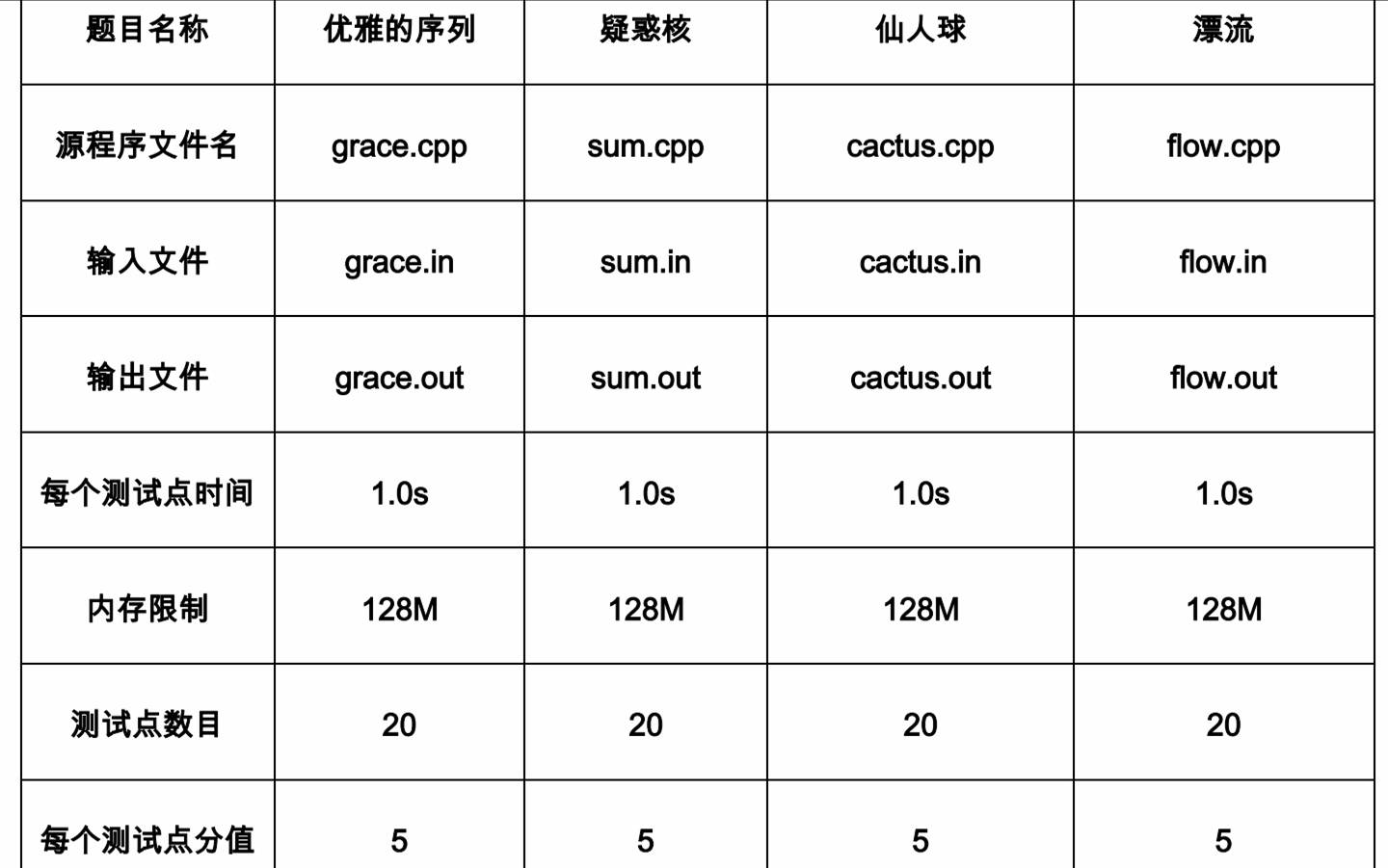
　　终于400了。这套题很鬼畜。两道贪心。

---

　　GRACE sort过后，不能直接统计，本人毫无多想，相同的直接放在一起。结果太多人AC。

　　SUM sigma+异或和（可使用前缀和处理），本人毫无考虑乱MOD，居然对了50分。（注意处理2^63-1）

 #define PN "sum"
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 template<class T>inline void readin(T &res) {
     static char ch;T flag = ;
     while((ch=getchar())<''||ch>'')if(ch=='-')flag=-;
     res=ch-;
     while((ch=getchar())>=''&&ch<='')res=(res<<)+(res<<)+ch-;
     res*=flag;
 }
 const long long MOD = 23333333333333333LL;
 long long calc[], K[];
 void CAL(long long a,long long delta) {
     long long k;a+=;
     for( long long bit = , pow = ; bit <= ; bit++,pow<<= ) {
         k=a/pow/*pow;
         calc[bit]=calc[bit]+(k+std::min(a-(k<<),pow))*delta;
     }
 }
 long long add(long long a,long long b) {return a+b>MOD?a+b-MOD:a+b;}
 long long cheng(long long a,long long b) {
     long long res;
     for(res=;a;a>>=,b=add(b,b)) if(a&) res=add(res,b);
     return res;
 }
 int main() {
     freopen(PN ".in","r",stdin);
     freopen(PN ".out","w",stdout);
     long long T, a, b, c;readin(T);
     for( long long bit = , pow = ; bit <= ; bit++,pow<<= ) K[bit]=pow%MOD;
     while(T--) {
         readin(a);readin(b);readin(c);
         memset(calc, , sizeof(calc));
         if(b==9223372036854775807LL) for( long long bit = ; bit <= ; bit++ ) calc[bit]=4611686018427387904LL;
         else CAL(b,);
         CAL(a-,-);
         long long ans = ;
         for( long long bit = , pow = ; bit<=; bit++,pow<<=,c>>= ) {
             if(c&) ans=(ans+cheng(calc[bit],K[bit]))%MOD;
             else ans=(ans+cheng(b-a+-calc[bit],K[bit]))%MOD;
         }
         printf("%lld\n",ans);
     }
     return ;
 }

SUM

　　CACTUS 大部分都是对的，直接倍增，并不苛求用链剖。注意点权下放后的处理。（两行的错误）

　　FLOW 贪心，无后效性，直接跑就完了！本人以为是DP+数据结构优化，虽然题解也这么写。

---

　　竟然最初只有55！不想说了，完毕。