poj1947（树形背包）

题目链接：http://poj.org/problem?id=1947

Rebuilding Roads

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 13501		Accepted: 6253

Description

The cows have reconstructed Farmer John's farm, with its N barns (1 <= N <= 150, number 1..N) after the terrible earthquake last May. The cows didn't have time to rebuild any extra roads, so now there is exactly one way to get from any given barn to any other barn. Thus, the farm transportation system can be represented as a tree.

Farmer John wants to know how much damage another earthquake could do. He wants to know the minimum number of roads whose destruction would isolate a subtree of exactly P (1 <= P <= N) barns from the rest of the barns.

Input

* Line 1: Two integers, N and P

* Lines 2..N: N-1 lines, each with two integers I and J. Node I is node J's parent in the tree of roads.

Output

A single line containing the integer that is the minimum number of roads that need to be destroyed for a subtree of P nodes to be isolated. 

Sample Input

11 6
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11

Sample Output

2

Hint

[A subtree with nodes (1, 2, 3, 6, 7, 8) will become isolated if roads 1-4 and 1-5 are destroyed.] 

 

题意：给你一颗有n个节点的树，问你最少去掉多少条边可以得到节点数m的子树

思路：一开始没认真看题目，以为题目是问从树上取出m个节点最少要多少条边（取出的节点可以不相连），然后就wa了。。。

看到这题，就很容易想出dp数组，dp[i][j]表示从以i为根节点 的子树中去点j个节点最少要去掉的边数

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct{//链式前向星
    int v,next;
}edge[];
int head[];
int dp[][];//dp[i][j]表示在i节点的子树里（不是以i组成的子树）去掉j个节点需要减少的最少的边数
int sum[];//sum[i]表示在i节点的子树里一个有多少个节点（不包括i）
int cnt;
void add(int u,int v){
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
/*
i节点的子树（不包括i）
以i节点为根组成子树（树）（包括i）
*/
int n,m;
void dfs(int k){
    sum[k]=;//初始化
    for(int i=;i<=n;i++)//初始化
    dp[k][i]=1e9;
    dp[k][]=;//无论是哪个点，去掉0个节点的花费一定是0
    for(int i=head[k];i!=-;i=edge[i].next){
            dfs(edge[i].v);//先向子节点搜索
            sum[k]+=sum[edge[i].v]+;//计算k节点的子树里有多少个节点
            dp[edge[i].v][sum[edge[i].v]+]=;//去除当前子节点为根组成树的所有的节点的花费一定是1（只需断开k与当前子节点的连接）
            //printf("%d %d %d\n",edge[i].v,sum[edge[i].v]+1,dp[edge[i].v][sum[edge[i].v]+1])    ;
            for(int j=n;j>;j--){ //为什么要j>0,因为j=0的花费一定是0，没必要更新
                for(int l=;l<=j;l++)
                dp[k][j]=min(dp[k][j],dp[k][j-l]+dp[edge[i].v][l]);
                /*为什么l从1开始，因为从0开始没必要（min(dp[k][j],dp[k][j]+dp[edge[i].v][0]);）它的
                结果一定是原来的dp[k][j],因为 dp[edge[i].v][0]=0，为什么l可以等于j，因为我可以当前的j个全部
                从当前子节点组成的子树去除*/
            }
    }
}
bool vt[];//标记数组
int main(){
    while(scanf("%d%d",&n,&m)!=EOF){
        int u,v;
        cnt=;
        fill(head,head+,false);//初始化
        fill(head,head+,-);
        for(int i=;i<n;i++){
            scanf("%d%d",&u,&v);
            add(u,v);
            vt[v]=true;
        }
        int root=;
        for(int i=;i<=n&&!root;i++){//找根节点
            if(!vt[i])
            root=i;
        }
        dfs(root);
        int ans=dp[root][n-m];//我要得到节点数为m的子树，需要去掉n-m个点
        for(int i=;i<=n;i++)
        if(sum[i]+>=m)
        ans=min(ans,dp[i][sum[i]+-m]+);//取以第i个节点为根节点组成的子树（包括i）时，先要减去他与父节点的连接，
        //然后再到子树里减去sum[i]+1-m个节点（因为以i为根组成的子树（树）只有sum[i]+1个节点）
        printf("%d\n",ans);
    } 

    return ;
}

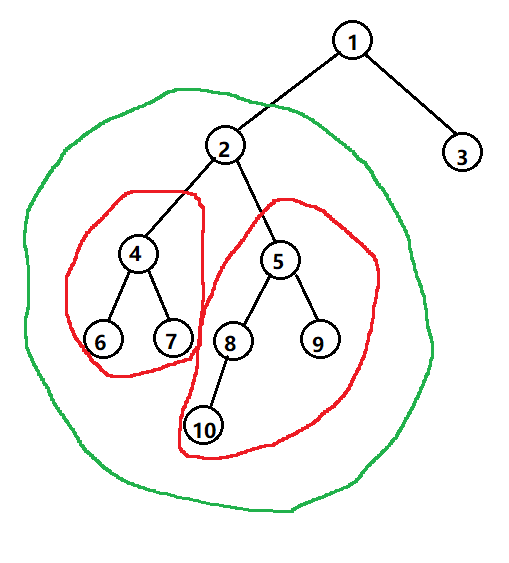
绿色的表示以2节点为根节点组成的子树

红色的表示2节点的子树