codeforces#410C Mike and gcd problem

题目：Mike and gcd problem

题意：给一个序列a₁到a_{n ,}如果gcd(a₁,a₂,...a_n)≠1,给一种操作，可以使a_i和a_i+1分别变为(a_i+a_i+1)和(a_i-a_i+1);问需要执行几次这个操作才能使得gcd(a₁,a₂,...a_n)>1.

分析：

1.首先，答案总是YES。

2，假设gcd(a₁,a₂,...a_n)=1，在一次对a_i和a_i+1的操作后新的gcd为d,则d满足：d|a_i - a_i + 1 and d|a_i + a_i + 1  d|2a_i and d|2a_i + 1.。同样，因为d是新序列的gcd,所以d也满足： d|a_j, j ≠ i, i + 1.

3.从而我们得到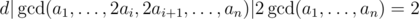：。所以gcd(a₁,a₂,...a_n)=1,则在一次操作后，序列的gcd最多会变得两倍大.(即会变成2.)

4.这意味着如果我们要是序列的gcd大于1的话只用使所有的数为偶数即可。

5.因为两个奇数只通过一次操作即都可以变成偶数，而一奇一偶要通过两次才可以都变成偶数。

6.可以把题目转化为：给一个序列a₁到a_{n ,}如果gcd(a₁,a₂,...a_n)≠1,求将所有数变成偶数需要的操作次数

7.又可转化为：求序列中有几段连续为奇数，如果使奇数段中含的数为偶数个k，则需要k/2次，如果为奇数个，则需要(k/2)+2次;

代码：

/*
Problem: C. Mike and gcd problem
Time: 2017/5/5/19:21
*/

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<map>
#include<vector>
#define ll long long
#define inf 100000000
using namespace std;

ll a[];
ll gcd(ll a,ll b)
{
    return b==?a:gcd(b,a%b);
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<n;i++)
        scanf("%I64d",a+i);
    ll d=a[];
    for(int i=;i<n;i++)
        d=gcd(d,a[i]);
    int ans=;
    if(d<=)
    {
        int odd=;
        for(int i=;i<n;i++)
        {
            if(a[i]%!=) odd++;
            else if(odd!=)
            {
                ans+=(odd%==?(odd/):(odd/+));
                odd=;
            }
        }
        //cout<<ans<<endl;
        if(odd) ans+=(odd%==?(odd/):(odd/+));
    }
    printf("YES\n");
    printf("%d\n",ans);
    return ;
}

补充：(关于DIVISIBILITY AND GREATEST COMMON DIVISORS)

几个定理：

1.. Let a, b ∈ Z with a|b. Then a|bc for any c ∈ Z.

2. If a|b and b|c then a|c.

3.If a|b and a|c then a|(br + cs) for every r and s in Z. In particular, if a|b and a|c then a|(b + c) and a|(b − c).

4.For nonzero a and b in Z, there are x and y in Z such that (3.2) (a, b) = ax + by.