深度学习中Xavier初始化

　　“Xavier”初始化方法是一种很有效的神经网络初始化方法，方法来源于2010年的一篇论文《Understanding the difficulty of training deep feedforward neural networks》。

文章主要的目标就是使得每一层输出的方差应该尽量相等。下面进行推导：每一层的权重应该满足哪种条件才能实现这个目标。

　　我们将用到以下和方差相关的定理：

假设有随机变量x和w，它们都服从均值为0，方差为σ的分布，且独立同分布，那么：

•      w*x就会服从均值为0，方差为σ*σ的分布

•      w*x+w*x就会服从均值为0，方差为2*σ*σ的分布

　　文章实验用的激活函数是tanh激活函数，函数形状如下左图，右图是其导数的函数形状。

从上图可以看出，当x处于0附近时，其导数/斜率接近与1，可以近似将其看成一个线性函数，即f(x)=x。

　　我们假设所有的输入数据x满足均值为0，方差为的分布，我们再将参数w以均值为0，方差为的方式进行初始化。我们假设第一层是卷积层，卷积层共有n个参数（n=channel*kernel_h*kernel_w），于是为了计算出一个线性部分的结果，我们有：

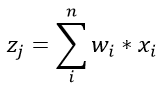
其中，忽略偏置b。

假设输入x和权重w独立同分布，我们可以得出z服从均值为0，方差为的分布，即

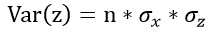
　　为了更好地表达，我们将层号写在变量的上标处，

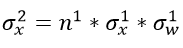
　　我们将卷积层和全连接层统一考虑成n个参数的一层，于是接着就有：

　　

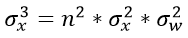
　　如果我们是一个k层的网络（这里主要值卷积层+全连接层的总和数），我们就有

　　继续展开，最终可以得到

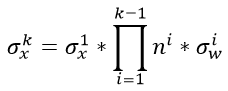
从上式可以看出，后面的连乘是非常危险的，假如说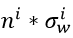总是大于1，那么随着层数越深，数值的方差会越来越大；如果乘积小于1，那么随着层数越深，数值的方差会越来越小。

我们再回头看看这个公式，

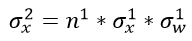
　　如果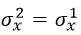，那么我们就能保证每层输入与输出的方差保持一致，那么应该满足：

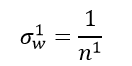
　　即对应任意第i层，要想保证输入与输出的方差保持一致，需要满足：

------------------------------------------------------------------------------------------------

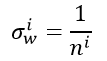
上面介绍的是前向传播的情况，那么对于反向传播，道理是一样的。

假设我们还是一个k层的网络，现在我们得到了第k层的梯度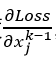，那么对于第k-1层输入的梯度，有

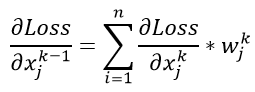
　　从上式可以看出K-1层一个数值的梯度，相当于上一层的n个参数的乘加。这个n个参数的计算方式和之前方式一样，只是表示了输出端的数据维度，在此先不去赘述了。

　　于是我们假设每一层的参数服从均值为0，方差为某值的分布，那么有如下公式：

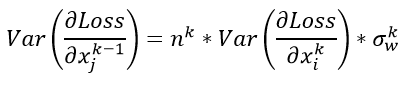
对于这个k层网络，我们又可以推导出一个的公式：

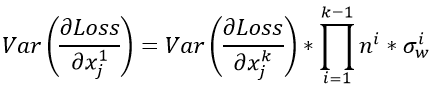
上式中连乘是非常危险的，前面说过，在此不在赘述（这就会造成梯度爆炸与梯度消失的问题，梯度爆炸与梯度消失可以参考这两篇文章）。我们想要做到数值稳定，使得反向传播前后的数值服从一个稳定的分布，即

那么需要满足如下条件：

-----------------------------------------------------------------

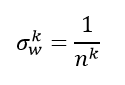
　　如果仔细看一下前向传播与反向传播的两个公式，我们就会发现两个n实际上不是同一个n。对于全连接来说，前向操作时，n表示了输入的维度，而后向操作时，n表示了输出的维度。而输出的维度也可以等于下一层的输入维度。所以两个公式实际上可以写作：

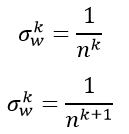
于是为了均衡考量，最终我们的权重方差应满足：

　　

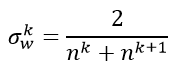
　　下面就是对这个方差的具体使用了。论文提出使用均匀分布进行初始化，我们设定权重要初始化的范围是[-a,a]。而均匀分布的方差为：

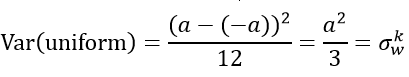
由此可以求得

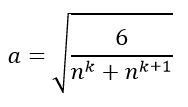
上面就是xavier初始化方法，即把参数初始化成下面范围内的均匀分布。

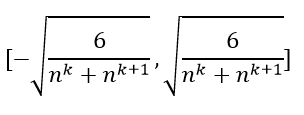
转载自：

CNN数值——xavier（上）：https://zhuanlan.zhihu.com/p/22028079

CNN数值——xavier（下）: https://zhuanlan.zhihu.com/p/22044472

深度学习——Xavier初始化方法：https://blog.csdn.net/shuzfan/article/details/51338178