洛谷 P2401 不等数列

其实有两种方法来解这道题
# 第一种：找规律（非正经）

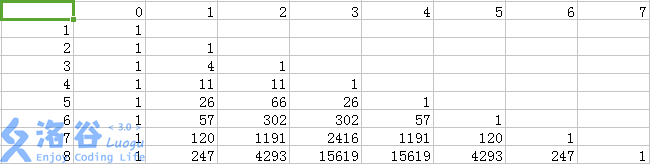
一看，这玩意像是个杨辉三角，还左右对称呢

因为新插入一个数$n$，有$n+1$个位置可以选，所以总数就乘$n+1$，对应的$f[n+1][i]$也就等于$f[n][i]$了大概。可是一看，不大对，好像不是这样。那么就像，反正加一个数要么没变，要么加一个小于号，那么不在$f[n+1][i]$的一定是分到了$f[n+1][i+1]$里去了。那么以$n=3$时为例,$f[3][1]*4=4,f[4][1]=1$也就是接收了$1$倍的$f[3][1]$。那么就有$3$个分到$f[4][2]$里去了。$f[3][2]*4=16,f[4][2]=11$，而$f[4][2]$已经有$3$个,那么就接收了来自$f[4][2]$的$8$个，也就是$2$倍的$f[3][2]$。······以此类推，大概就得出了$f[n+1][i]+=f[n][i]*(i+1),f[n+1][i+1]+=f[n][i]*(n-i)$的规律

-----------------------------------------------手动分割线------------------------------------------------

# 第二种：数学方法推
**这是正经方法**

前面说过，加入一个数$n$，有$n$+$1$个位置可以选，可以插在两旁或者不等号的位置，因为新插入的数一定是最大的，所以插在最左边多一个大于号，而插在最右边多一个小于号。

那么问题来了，如果插在不等号的位置呢？

首先，明确一下，插入在不等号位置后，一个不等号会变为两个不等号，由于新插入的数一定是最大的，所以这两个不等号中前面的一定是小于号，后面的一定是大于号。那么就很明显了，如果这个位置原来是小于号，那么插入$n$之后，小于号数不变；如果原来是大于号，那么插入$n$之后，小于号数+$1$。那么原本有$i$个数$j$个小于号，加上一个数后便会有$j+1$种小于号不变$i-j$种小于号$+1$的情况。

上代码

先是**暴力版**（通不过的，这是帮助我打出那张图的版本）
```cpp
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=1005;
int f[maxn],n,ans[maxn];
bool s[maxn];
void dfs(int step){
if(step>n){
int sum=0;
for(int i=1;i<n;i++)sum+=f[i]<f[i+1]?1:0;
ans[sum]++;
return;
}
for(int i=1;i<=n;i++)
if(!s[i]){
s[i]=1;
f[step]=i;
dfs(step+1);
s[i]=0;
}
}
int main(){
scanf("%d",&n);
dfs(1);
for(int i=0;i<n;i++)printf("%d ",ans[i]);
}
```

然后上
## 正常版本
```cpp
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int maxn=1005;
int n,k,f[maxn][maxn];
int main(){
//freopen("num.in","r",stdin);
//freopen("num.out","w",stdout);
scanf("%d%d",&n,&k);
if(k>(n-1)/2)k=n-k-1;
f[1][0]=1;
for(int i=1;i<n;i++){
for(int j=0;j<=(i-1)/2;j++){//由于它类似于杨辉三角，左右对称，所以只求左侧就好
f[i+1][j]=(f[i+1][j]+f[i][j]*(j+1))%2015;
f[i+1][j+1]=(f[i+1][j+1]+f[i][j]*(i-j))%2015;
}
if(i%2==0)f[i+1][i/2]=(f[i+1][i/2]*2)%2015;
}
printf("%d",f[n][k]);
return 0;
}
```
**不喜勿喷**
### 请勿抄袭