「洛谷P1196」「NOI2002」银河英雄传说 解题报告

P1196 [NOI2002]银河英雄传说

题目描述

公元五八○一年，地球居民迁至金牛座α第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历七九九年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成\(30000\)列，每列依次编号为\(1, 2, …,30000\)。之后，他把自己的战舰也依次编号为\(1, 2, …, 30000\)，让第\(i\)号战舰处于第\(i\)列\((i = 1, 2, …, 30000)\)，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为\(M_{i,j}\)，含义为第i号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：\(C_{i,j}\)。该指令意思是，询问电脑，杨威利的第ii号战舰与第jj号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

最终的决战已经展开，银河的历史又翻过了一页……

输入输出格式

输入格式：

第一行有一个整数\(T(1 \le T \le 500,000)\)，表示总共有TT条指令。

以下有\(T\)行，每行有一条指令。指令有两种格式：

1. \(M_{i,j}\) ：\(i\)和\(j\)是两个整数\((1 \le i,j \le 30000)\)，表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第ii号战舰与第jj号战舰不在同一列。
2. \(C_{i,j}\) ：\(i\)和\(j\)是两个整数\((1 \le i,j \le 30000)\)，表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出格式：

依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第\(i\)号战舰与第\(j\)号战舰之间布置的战舰数目。如果第\(i\)号战舰与第\(j\)号战舰当前不在同一列上，则输出\(-1\)。

输入输出样例

输入样例#1：

4
M 2 3
C 1 2
M 2 4
C 4 2

输出样例#1：

-1
1

说明

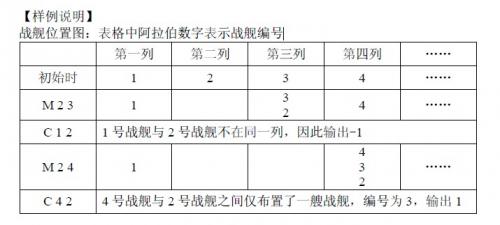
【样例说明】

战舰位置图：表格中阿拉伯数字表示战舰编号

---

写在前面

这是一道边带权并查集的好题。(我的题解可能对不了解并查集的人不太友好)

思路

我们很容易想到记录每只船在某处排行位置，然后询问时直接减一减就可以了。就这样，问题转换为如何保留每个数的位置(d[i])。

Hint:注意，为了方便，我们把d[i]记作相对f[i]的位置。

当一列船(记为A 首只船为 a)合并到另一列(记为B 首只船为b)时，我们为了让a直接以b为父亲，我们要记录每一列船的只数(s[i])，将d[a]修改为s[a] + 1(连到最后时rank为原来船数+1)，别忘了修改s[b]与f[a]的值。对于后面父亲不为B的先不管。当寻找祖先时，对于父亲是祖先的船，我们不用修改，因为在合并时已经修改过了，而对于父亲不是祖先的船，我们可以先修改它的父亲(递归进行)，是他的父亲的父亲为它的老祖宗，然后把它的d[i] = d[i] + d[f[i]];这样就把参照物改为他的祖宗，实现了路径压缩。

代码很短，只有一点点。。。

代码

#include<bits/stdc++.h>
using namespace std;
#define N 30000

int T;
int f[N + 5], d[N + 5], s[N + 5];

int find( int x ){
	if ( f[x] == x ) return x;
	int fa(find(f[x]));
	d[x] = d[x] + d[f[x]] - 1;
	return f[x] = fa;
}

void Merge( int x, int y ){
	x = find(x); y = find(y);
	if ( x == y ) return;
	f[x] = y; d[x] = s[y] + 1; s[y] += s[x];
}

int main(){
	scanf( "%d", &T );
	for ( int i = 1; i <= N; ++i ) f[i] = i, d[i] = 1, s[i] = 1;
	while( T-- ){
		char t; int x, y;
		while( ( t = getchar() ) != 'M' && t != 'C' );
		scanf( "%d%d", &x, &y );
		if ( t == 'M' ) Merge( x, y );
		else{
			if ( find(x) == find(y) ){
				if ( x == y ) printf("0\n");
				else if ( d[x] > d[y] ) printf( "%d\n", d[x] - d[y] - 1 );
				else printf( "%d\n", d[y] - d[x] - 1 );
			} else printf( "-1\n" );
		}
	}
	return 0;
}