meet-in-the-middle 基础算法（优化dfs）

　　 $meet-in-the-middle$（又称折半搜索、双向搜索）对于$n<=40$的搜索类型题目，一般都可以采用该算法进行优化，很稳很暴力。

　　$meet-in-the-middle$算法的主要思想是将搜索区域化为两个集合，分别由搜索树的两端向中间扩展，直到搜索树产生交集，此时即可得到我们的合法情况。

　　通常适用于求经过$n$步变化，从A集合变到B集合需要的方案数问题。

　　对于普通dfs来说，其一大弊端是随着搜索层数的不断增加，搜索的复杂度也会极速增长，

　　而$meet-in-the-middle$算法能够将搜索层数降至原来的一半，对整体效率而言无疑是不小的提升。

　　如图所示：

　　　　　　

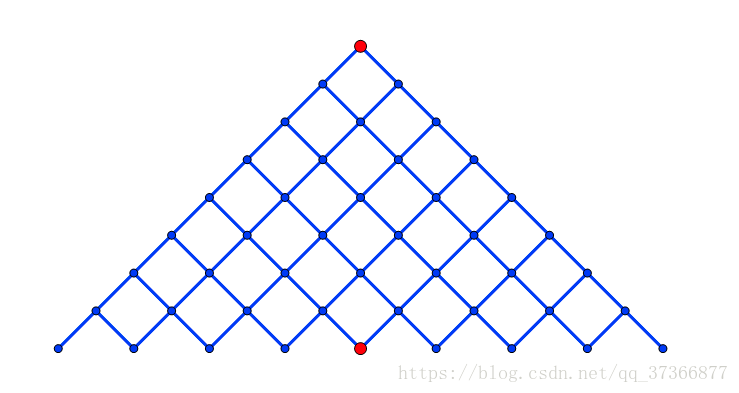
　　可以明显看出$meet-in-the-middle$对于dfs优化之显著。

　　那么考虑$meet-in-the-middle$的算法流程：

　　　　1、从状态$L$出发，经过$x$步状态扩展，记录到达状态$i$的步数，通常这里会与状压、二分等内容结合。

　　　　2、从状态$R$出发，经过$y$步状态扩展，若同样到达状态$i$并且步数不为0，则累加答案。

　　通常我们需要保证$x+y=n$，也就是需要满足状态总数不变，只是深度减少，一般情况下取$x=y=(n>>1)$最优

　　但具体情况应视题而定，可能搜索深度不均匀时，效率反而会更高。

　　

　　下面来看一道例题：

　　[BZOJ 2679] Balanced Cow Subsets

　　简要题意：有多少个非空子集,能划分成和相等的两份。$(n<=20)$

　　分析：显然的$meet-in-the-middle$定义，考虑如何转化

　　将题设转化成方程的形式$a1x1+a2x2+a3x3+...+anxn=0$，其中$x=0,1,-1$（表示不选，选入集合$l$，选入集合$r$），那么移项可得一种两侧各有一种集合的形式，根据题目要求，我们需要求出可以构建出该方程的集合方案数，可以采用状压的思想，记录所选取的数的和以及选取集合的状态即可。

　　

#include<bits/stdc++.h>
#include<tr1/unordered_map>
#define re register
using namespace std;
int n,a[],cntl,cntr,ans=-;
bool vis[<<];
inline int read(){
    re int a=,b=; re char ch=getchar();
    while(ch<''||ch>'')
        b=(ch=='-')?-:,ch=getchar();
    while(ch>=''&&ch<='')
        a=(a<<)+(a<<)+(ch^),ch=getchar();
    return a*b;
}
struct node{
    int sta,val; node(){}
    node(int x,int y){sta=x,val=y;}
    bool operator < (const node &b) const {
        return val<b.val;
    }
    bool operator > (const node &b) const {
        return val>b.val;
    }
}l[<<],r[<<];
inline void dfs1(re int x,re int tot,re int sta){
    if(x>(n>>)){
        l[++cntl]=node(sta,tot);
        return ;
    }
    dfs1(x+,tot,sta);
    dfs1(x+,tot+a[x],sta|(<<(x-)));
    dfs1(x+,tot-a[x],sta|(<<(x-)));
}
inline void dfs2(re int x,re int tot,re int sta){
    if(x>n){
        r[++cntr]=node(sta,tot);
        return ;
    }
    dfs2(x+,tot,sta);
    dfs2(x+,tot+a[x],sta|(<<(x-)));
    dfs2(x+,tot-a[x],sta|(<<(x-)));
}
signed main(){
    n=read();
    for(re int i=;i<=n;++i) a[i]=read();
    dfs1(,,); dfs2((n>>)+,,);
    sort(l+,l+cntl+,less<node>());
    sort(r+,r+cntr+,greater<node>());
    for(re int i=,j=,pos;i<=cntl&&j<=cntr;++i){
        while(j<=cntr&&l[i].val+r[j].val>)  ++j;
        for(pos=j;l[i].val==-r[pos].val;++pos){
            re int sta=(l[i].sta|r[pos].sta);
            if(!vis[sta]) vis[sta]=,++ans;
        }
    }
    printf("%d\n",ans);
}

Code

　　

　　 同种类的题目还有许多，例如  [POJ 1186] 方程的解数，  [BZOJ 4800] 冰球世界锦标赛  等。

　   综上可见$meet-in-the-middle$算法的应用之广。

　   至此，通过分析转化搜索模型，达到了降低搜索复杂度，优化程序效率的目的。