DAG及拓扑排序

1.有向无环图和拓扑排序

有向无环图(Directed Acyclic Graph，简称DAG)；拓扑排序指的对DAG一个有序的线性排列。即每次选出一个没有入度的节点，然后输出该点并将节点和其相关连的弧都删除(此时均为以该节点为弧头的弧)，依次进行，直至遍历所有节点，就是一个DAG的拓扑排序，值得一提的是一个图的拓扑排序不一定是唯一的，很有可能有若干个排序。不过这样仍然不太清楚，我们以图来展示。

                                        

                                                     

                                                      

                                                                                                       

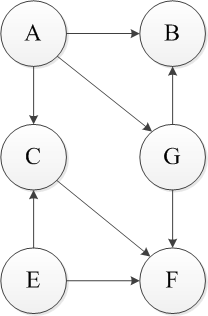
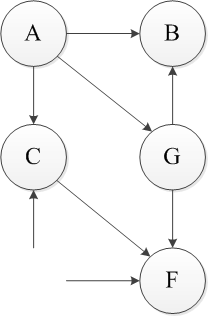
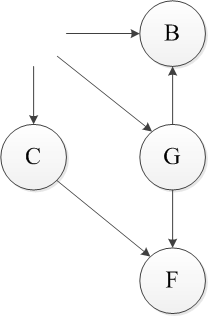
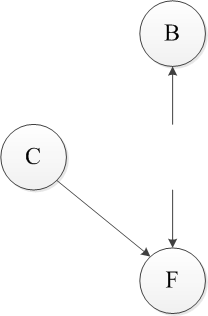
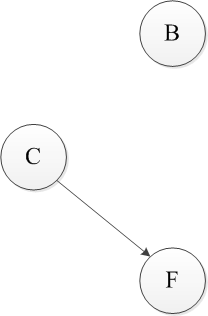
上述过程即为一个拓扑排序，首先对于该DAG来说，只有A和E是无入度的节点，任选一个E删除，接着删除相应的弧。【输出E】

同样此时只有A变成无入度节点，做同样的操作。【输出A】

删除A后只有顶点C和G没有前驱，仍然任选一个删除，依此类推，可以得到一个该图的拓扑排序。EAGCFB

2.拓扑排序的实现
前面深搜广搜已经用邻接矩阵实现无向图了，这里我们使用邻接表来表示有向图。先来复习一下邻接表

对于这样的数据结构应该怎么实现呢？如果你第一眼看上去觉得这就是若干个链表组成的，那么恭喜你回答正确，我们一般都是使用链表的思想来实现邻接表的。因此我们首先要在域中定义一个链表的数组：

    private Ljtable [] vertex;

然后定义链表和节点类

    class Ljtable {
        char data;
        Node head;
 
        public  Ljtable(char c,int n)
        {
            data = c;
            head = new Node(n);
        }
    }
 
    class Node {
        int number;
        Node next;
        public Node(int a)
        {
            number = a;
            next = null;
 
        }
    }

拓扑排序，纯本人手写，因为我的代码会使各节点的入度发生变化，因此需要提前存储，拓扑排序后在复原，看起来有点蠢。不过由于都是顺序排列，所以时间复杂度还好。

    public void Topo()
    {
        int [] m = new int [vertex.length];
        for (int i = 0; i < vertex.length; i++)
        {
            m[i] = vertex[i].inDegree;
        }
 
        int k = 0;
        while(k < vertex.length)
        for (Ljtable l:vertex)
        {
            if(l.inDegree == 0) {
                System.out.print(l.data);
                k++;
                Node h = l.head;
                while(h!=null) {
                    vertex[h.number].inDegree--;
                    h = h.next;
                }
            }
 
        }
 
        for (int i = 0; i < vertex.length; i++)
        {
             vertex[i].inDegree  =  m[i];
        }
 
}

完整代码请看这里。