[Algorithms] Graph Traversal (BFS and DFS)

Graph is an important data structure and has many important applications. Moreover, grach traversal is key to many graph algorithms. There are two systematic ways to traverse a graph, breadth-first search (BFS) and depth-frist search (DFS).

Before focusing on graph traversal, we first determine how to represent a graph. In fact, there are mainly two ways to represent a graph, either using adjacency lists or adjacency matrix.

An adjacency list is an array of lists. Each list corresponds to a node of the graph and stores the neighbors of that node.

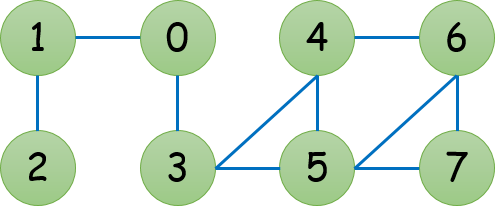
For example, for the (undirected) graph above, its representation using adjacency lists can be:

0: 1 -> 3 -> NULL

1: 0 -> 2 -> NULL

2: 1 -> NULL

3: 0 -> 4 -> 5 -> NULL

4: 3 -> 5 -> 6 -> NULL

5: 3 -> 4 -> 6 -> 7 -> NULL

6: 4 -> 5 -> 7 -> NULL

7: 5 -> 6 -> NULL

An adjacency matrix is a matrix of size m by m (m is the number of nodes in the graph) and the (i, j)-the element of the matrix represents the edge from node i to node j.

For the same graph above, its representation using adjacency matrix is:

0 1 0 1 0 0 0 0

1 0 1 0 0 0 0 0

0 1 0 0 0 0 0 0

1 0 0 0 1 1 0 0

0 0 0 1 0 1 1 0

0 0 0 1 1 0 1 1

0 0 0 0 1 1 0 1

0 0 0 0 0 1 1 0

In this passage, we use adjacency lists to represent a graph. Specifically, we define the node of the graph to be the following structure:

 struct GraphNode {
     int label;
     vector<GraphNode*> neighbors;
     GraphNode(int _label) : label(_label) {}
 };

Now let's move on to BFS and DFS.

As suggested by their names, BFS will first visit the current node, then its neighbors, then the non-visited neighbors of its neighbors... and so on in a breadth-first manner while DFS will try to move as far as possible from the current node and backtrack when it cannot move forward any more (all the neighbors of the current node has been visited).

The implementation of BFS requries the use of the queue data structure while the implementation of DFS can be done in a recursive manner.

For more details on BFS and DFS, you may refer to Introduction to Algorithms or these two nice videos: BFS video and DFS video.

In my implementation, BFS starts from a single node and visits all the nodes reachable from it and returns a sequence of visited nodes. However, DFS will try to start from every non-visited node in the graph and starts from that node and obtains a sequence of visited nodes for each starting node. Consequently, the function bfs returns a vector<GraphNode*> while the function dfs returns a vector<vector<GraphNode*> >.

I also implement a function read_graph to input the graph manually. For the above graph, you first need to input its number of nodes and number of edges. Then you will input each of its edge in the form of "0 1" (edge from node 0 to node 1).

The final code is as follows.

 #include <iostream>
 #include <vector>
 #include <queue>
 #include <unordered_set>

 using namespace std;

 struct GraphNode {
     int label;
     vector<GraphNode*> neighbors;
     GraphNode(int _label) : label(_label) {}
 };

 vector<GraphNode*> read_graph(void) {
     int num_nodes, num_edges;
     scanf("%d %d", &num_nodes, &num_edges);
     vector<GraphNode*> graph(num_nodes);
     for (int i = ; i < num_nodes; i++)
         graph[i] = new GraphNode(i);
     int node, neigh;
     for (int i = ; i < num_edges; i++) {
         scanf("%d %d", &node, &neigh);
         graph[node] -> neighbors.push_back(graph[neigh]);
         graph[neigh] -> neighbors.push_back(graph[node]);
     }
     return graph;
 }

 vector<GraphNode*> bfs(vector<GraphNode*>& graph, GraphNode* start) {
     vector<GraphNode*> nodes;
     queue<GraphNode*> toVisit;
     unordered_set<GraphNode*> visited;
     toVisit.push(start);
     visited.insert(start);
     while (!toVisit.empty()) {
         GraphNode* cur = toVisit.front();
         toVisit.pop();
         nodes.push_back(cur);
         for (GraphNode* neigh : cur -> neighbors) {
             if (visited.find(neigh) == visited.end()) {
                 toVisit.push(neigh);
                 visited.insert(neigh);
             }
         }
     }
     return nodes;
 }

 bool visitAllNeighbors(GraphNode* node, unordered_set<GraphNode*>& visited) {
     for (GraphNode* n : node -> neighbors)
         if (visited.find(n) == visited.end())
             return false;
     return true;
 }

 void dfs_visit(vector<GraphNode*>& graph, GraphNode* node, \
                unordered_set<GraphNode*>& visited, vector<GraphNode*>& tree, \
                vector<vector<GraphNode*> >& forest) {
     visited.insert(node);
     tree.push_back(node);
    if (visitAllNeighbors(node, visited)) {
         forest.push_back(tree);
         tree.clear();
         return;
     }
     for (GraphNode* neigh : node -> neighbors)
         if (visited.find(neigh) == visited.end())
             dfs_visit(graph, neigh, visited, tree, forest);
 }

 vector<vector<GraphNode*> > dfs(vector<GraphNode*>& graph) {
     vector<GraphNode*> tree;
     vector<vector<GraphNode*> > forest;
     unordered_set<GraphNode*> visited;
     for (GraphNode* node : graph)
         if (visited.find(node) == visited.end())
             dfs_visit(graph, node, visited, tree, forest);
     return forest;
 }

 void graph_test(void) {
     vector<GraphNode*> graph = read_graph();
     // BFS
     printf("BFS:\n");
     vector<GraphNode*> nodes = bfs(graph, graph[]);
     for (GraphNode* node : nodes)
         printf("%d ", node -> label);
     printf("\n");
     // DFS
     printf("DFS:\n");
     vector<vector<GraphNode*> > forest = dfs(graph);
     for (vector<GraphNode*> tree : forest) {
         for (GraphNode* node : tree)
             printf("%d ", node -> label);
         printf("\n");
     }
 }

 int main(void) {
     graph_test();
     system("pause");
     return ;
 }

If you input the above graph to it as follows (note that you only need to input each edge exactly once):

The output will be as follows:

 BFS:

 DFS:

You may check it manually and convince yourself of its correctness :)