MLP 之手写数字识别

0. 前言

前面我们利用 LR 模型实现了手写数字识别，但是效果并不好（不到 93% 的正确率)。 LR 模型从本质上来说还只是一个线性的分类器，只不过在线性变化之后加入了非线性单调递增 sigmoid 函数进行一一映射。实际上，这里的非线性变换对于我们分类来说是几乎没有什么作用的（在分类上，它等价于线性变换之后挑选出输出值最大的节点作为我们的预测结果），于是我们考虑用更复杂一点的带有一个隐层的 MLP (Multi-Layer Perceptron) 模型。

1. 模型

MLP 模型可以看作是在输入空间经过非线性变换（第一层与第二层）之后的 LR（第二层与第三层）， MLP 的优势在于，一个经过训练的 MLP 的可以由第一层的输入经过非线性变换映射到另外一个线性可分的由隐层节点组成的空间里去。由于activation function 可以取很多种类型 (excluding polynomials)， a two-layer net work with linear outputs can uniformly approximate any continuous function on a compact input domain to arbitrary accuracy provided the network has a sufficiently large number of hidden units, 隐层这种优良的表现能力，也是 deeplearning 的基础。

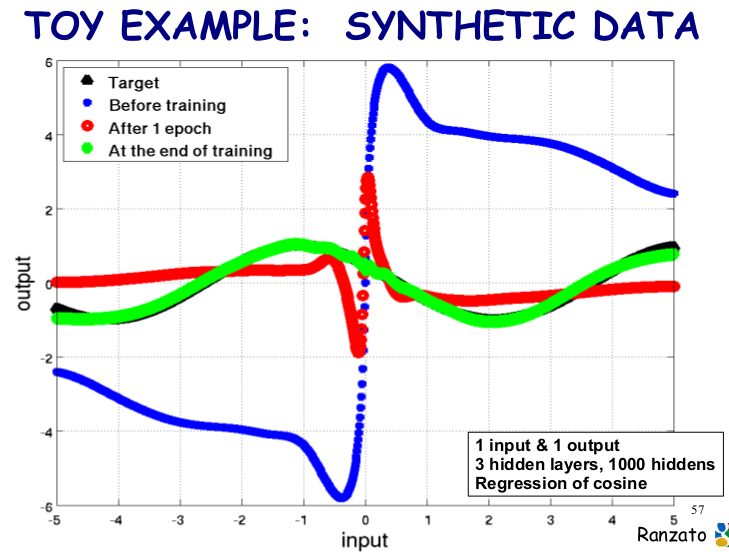
下面我们来看看具有 3 个隐层， 1000 个隐层节点的神经网络对 cos 函数的回归效果：

理解了前面两篇博客，对 bp 算法有了直观理解，明白了反向求导过程，再来看这个程序就变得非常简单了。在这个程序里面，我们的 MLP 模型可以表示如下：

用公式可以表示成：

这个模型包含的参数包括:

如果利用 SGD 来学习这个模型，我们需要知道 Loss Function (程序中加入了 L1 和 L2 范式）对于每个参数的偏导值。这里，我们可以采用前面已经介绍过的 BP 算法（BP 算法其实就是计算 ANN 中各个参数导数的一种快速算法，就像 FDCT 对于 DCT 的快速计算。在 Theano 库里面，由于函数是自动求导的，所以在下面的代码中我们几乎看不到 BP 的具体实现过程，我猜想 BP 过程应该是 Theano 自动完成的）。

2. 构建

只带有一个隐层的 MLP 的 hidden layer 到 output layer 在结构上与 LR 没有多大的差别。我们可以在之前的 LR 基础上添加从 input layer 到 hidden layer 的结构，就构成了这一小节中的 MLP。于是乎，我们构建了一个隐层节点，隐层的非线性函数设定为 tanh 函数(由 sigmoid 函数往下平移 0.5 再将值域扩大 2 倍)。对于隐层节点为 tanh 函数的神经网络来说， MLP 的权重空间具有很强的对称性，假设某一个解是 MLP 的最优解，那么：

将任意一个隐层节点的前后权重同时乘以 -1, 输出值不变，如果有 M 个 hidden units，那么就有对应的 2^M 次方个等价的解。
将 M 个隐层连同它连接的权重进行不同的排列组合，最后的输出也是等价的，这里对应有 M! 个等价的解。

这样，只有一个隐层的 MLP ，如果隐层节点采用 tanh 函数，那么权重空间就有 M!2^M 个等价的解。

全零向量正好处在解的对称中心，梯度为 0, 不能作为权重的初始值，所以需要对权重进行随机初始化，随机范围与 activation function 相关，有论文推导这一范围，暂时来不及细看。

接着我们把刚刚建立的隐层结构的输出作为 LR 的输入 (在 theano 里面实现十分简洁， graph structures 的方式真是太方便啦），这样，一个 MLP 的神经网络就搭好了。

3. 值得深入的地方

有些参数很难用梯度下降法进行优化， partly because some parameters are discrete values and others are real-valued. 并且由于优化的目标函数是非凸的，寻找极小值的工作量非常大，这些问题在 Yann LeCun 的论文有很好的 overview。
tanh 相对于 sigmoid 函数有什么优势？
权重初始化的范围。如何既保证初始时梯度最大，有保障 FP 和 BP 阶段信息 (variance) 良好的传递性？
learning rate 如何确定？是选择一个常量还是选择一个与迭代次数有关的变量？如果选常量，与什么因素有关？
隐层节点数目如何确定？一般来说，输入的 data set distribution 越复杂，需要的网络“容量”越大，隐层节点数目越多。
Regularizaiton Parameter 如何确定才能不至于导致模型太 underfitting or overfitting？

这是源代码下载地址，具体细节就不介绍了。用这种方法进行手写数字识别，在 5w 张图片上进行 828 次迭代训练，正确率可以达到 98.35%, 相比 LR 模型，的确是一个很大的提升！

参考资料：

[1]: deeplearning tutorial
[2]: PRML, Bishop, chapter 05

by：daniel-D

from：http://www.cnblogs.com/daniel-D/