nCOV 数据简要分析 (0326)

matlabdatacov

简介

碰巧看到了数据上传, 正在跑数据的我想着要不拟合一下看看, 然后, 就做了两个小时, 这里做一个简单的记录过程, 后续可能做在线的实时预测,,(坑...)

这个结果还是不能乱发的, 不然下一个谣言就是我了, 狗命要紧..

时代的一粒尘,落到个人身上就是一座大山,偏偏我们生活在尘土飞扬的时代

------ 方方

灾难并不是死了两万人这样一件事，而是死了一个人这件事，发生了两万次

-------北野武

这是灾难给我的印象最深的两句话, 愿逝者安息, RIP

获取数据

目前数据很多, 我比较信赖的是 JHU 给的一个全球的数据集 CSSEGISandData/COVID-19 数据^[1], 也有更为详细的国内的数据集比如 DXY-COVID-19-Data^[2], 相信之后也会有很多人进行数据分析,

我这边使用的是 2020年3月25日归档数据

数据整理

拿到数据之后是一个 502x66的数据, 包括全世界省/州 62天来的时间序列数据, 有着国家/省/经纬度以及时间序列

部分数据示例

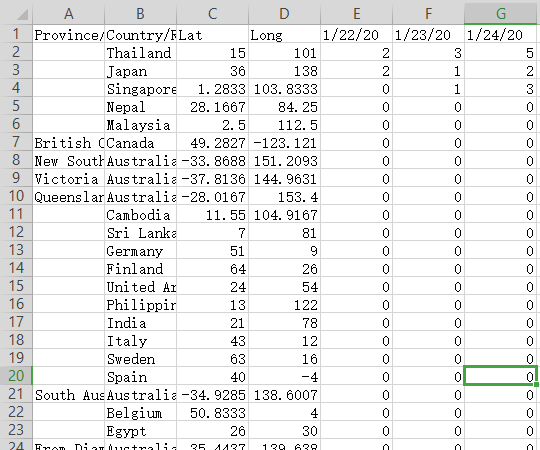
我们不做具体的每个地区的分析, 这里直接纵向累加即可, 最终得到的数据是 501x62 尺寸的数据

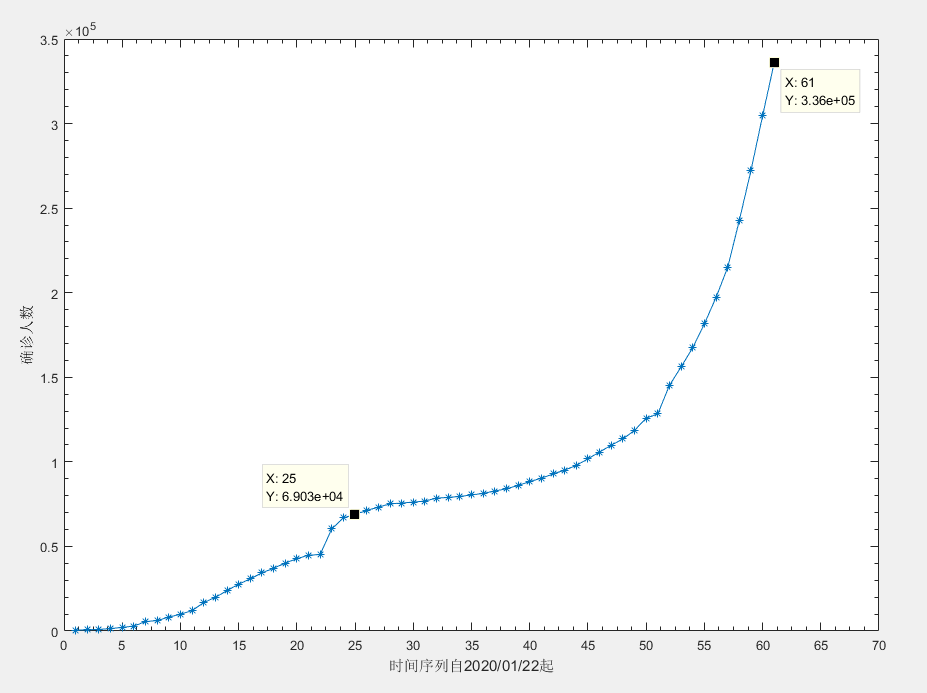
进而累加之后进行时间序列的绘制

这里为了顺手所以这边分析暂时都是使用的 MATLAB

自2020-1-22的全球确诊数据

数据拟合

这里避免一些数据问题, 我这单独标记出来了自 25天的数据,

在这之前的数据只有中国的, 这里只取后面的数据进行分析,

第25天也就是 2020年2月16日的数据,

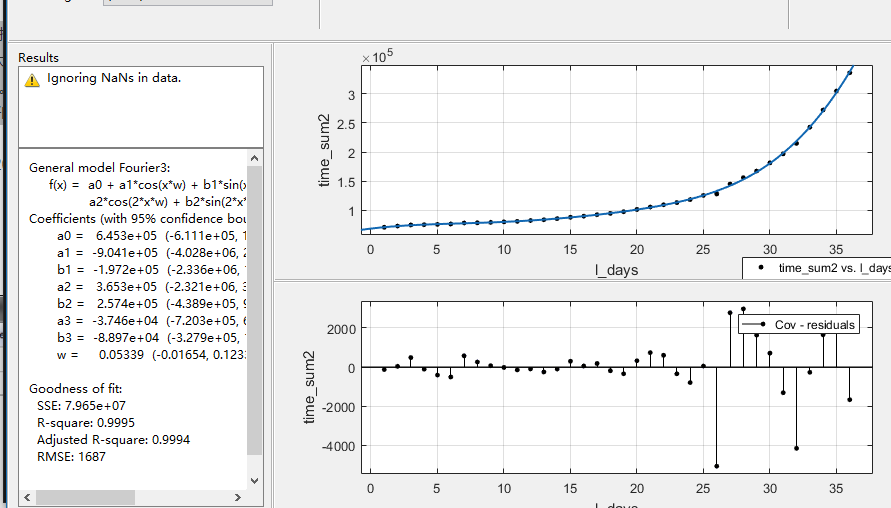
这里使用了 MATLAB 的 cftool 进行曲线拟合^[3]

具体的使用方法见参考链接

这边使用的是二次的指数拟合

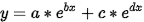
最终得到的结果如图

2月16号之后拟合数据

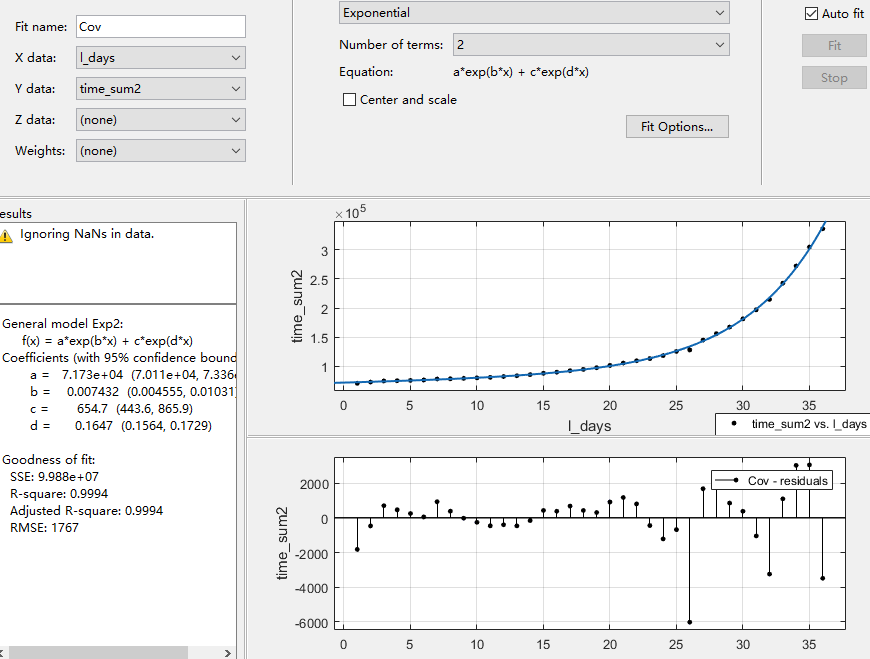
最终的到的拟合结果三组结果都可以, 一般取第一组数据

General model Exp2:
f(x) = a*exp(b*x) + c*exp(d*x)
Coefficients (with 95% confidence bounds):
a = 7.173e+04 (7.011e+04, 7.336e+04)
b = 0.007432 (0.004555, 0.01031)
c = 654.7 (443.6, 865.9)
d = 0.1647 (0.1564, 0.1729)
Goodness of fit:
SSE: 9.988e+07
R-square: 0.9994
Adjusted R-square: 0.9994
RMSE: 1767

SSE :错误的平方和。此统计量测量响应的拟合值的偏差。接近0的值表示更好的匹配。

R-square ：多重测定系数。数值的大小在0到1之间，越接近1，表明方程的变量对y的解释能力越强。

Adjusted R-square ：自由度调整 r 平方。接近1的值表示更好的匹配。当您向模型中添加附加系数时, 它通常是适合质量的最佳指示器。

RMSE ：均方根误差。接近0的值表示更好的匹配。

这里这个数据拟合的已经很好了, 测试发现使用 傅里叶多项式3次以上也能很好的拟合或者高斯4次以上都能很好的拟合, 拟合得到的相似程度已经很接近了, 如果单纯的数据分析已经足够了, 真的要去做的话还是要用医学模型进行分析, 这里只是简单的做以下

傅里叶三次曲线拟合

数据预测

有了数据曲线之后能做的事情就很多了, 按照得到的曲线方程进行后续拟合, 然后看什么时候能够达到 100W 的数据大关

确诊数据分析与预测

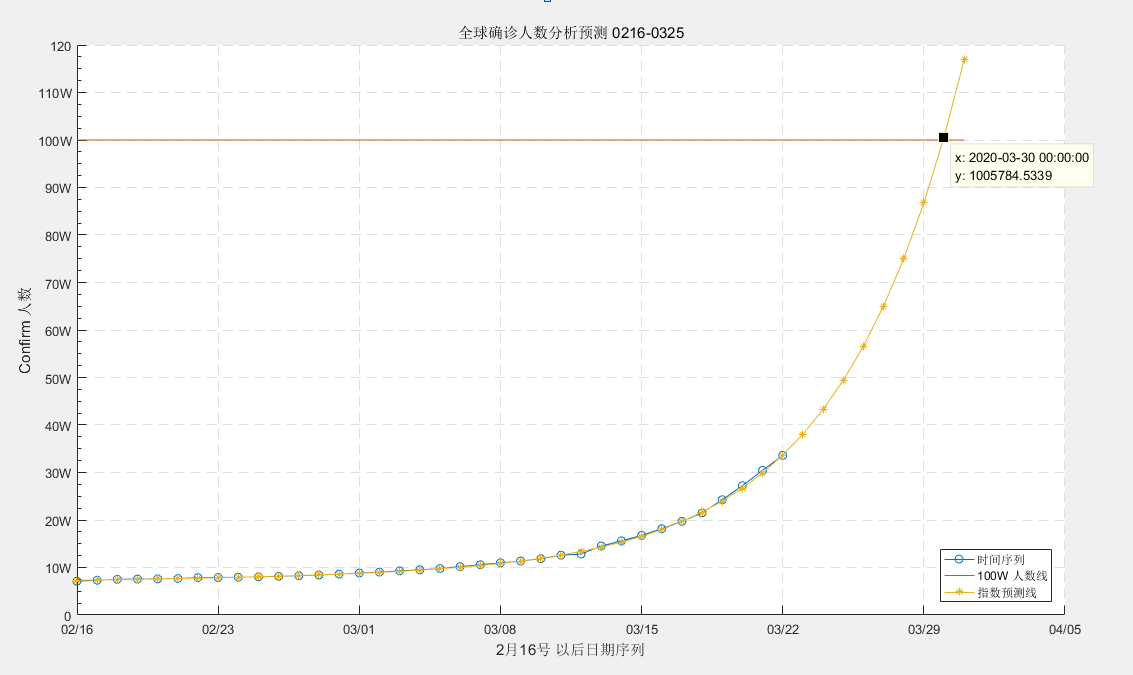
如果单纯从数据的角度考虑, 数据拟合的是没有问题的 , 数据显示大改会在 03/30号那天数据会超过 100W的情况,

数据仅供参考, 没有任何意义

其他

这个结果没有任何意义, 实际上的模型要复杂很多, 我希望这个数据从明天就不再继续增加了, 然后所有人都恢复健康,

希望数据不会成真, 但是我预感这个数据很可能会突破 100W, 应该在4月份的上旬或者中旬左右,

愿逝者安息, 世间平平安安

代码

最终附带分析代码

% COV data an
[city,day] = size(serial);
time_sum = zeros(1,day);
for i=1:day
time_sum(1,i) = sum(serial(:,i));
end
plot(time_sum,'-*');
days = 1:day;
d = 25;
l_days = 1:day-d;
for i=1:day-d
time_sum2(1,i) = sum(serial(:,i+d));
end
time_sum2 = time_sum2 - time_sum2(1);
% 运行 2月16号之后的数据
figure
hold on
% 从第25天的数据也就是 02/16日开始
init_day = datetime(2020,02,15);
t1 = init_day + l_days;
plot(t1,time_sum2,'-o');
% 绘制拟合曲线
a = 7.173e+04;
b = 0.007432;
c = 645.7;
d = 0.1647;
set_day = 45;
hold on
x = 1:set_day;
y= a*exp(b*x)+c*exp(d*x);
% 绘制 10000000 边界线
y_max = 1000000*ones(1,set_day);
plot(t,y_max);
% 绘制预测线
t = init_day+(x);
plot(t,y,'-*');
% 创建 xlabel
xlabel({'2月16号以后日期序列'});
datetick('x',6);
% 创建 ylabel
ylabel('Confirm 人数');

参考链接

2020-03-25 数据存档

CSSEGISandData/COVID-19 https://github.com/CSSEGISandData/COVID-19 ↩
DXY-COVID-19-Data https://github.com/BlankerL/DXY-COVID-19-Data ↩
matlabcftool用法及其菜单 https://blog.csdn.net/misskissC/article/details/8797655 ↩