【two pointers 细节题】cf1041dD. Glider

像这样细节老是打挂不行啊……

A plane is flying at a constant height of hh meters above the ground surface. Let's consider that it is flying from the point (−109,h)(−109,h) to the point (109,h)(109,h) parallel with OxOx axis.

A glider is inside the plane, ready to start his flight at any moment (for the sake of simplicity let's consider that he may start only when the plane's coordinates are integers). After jumping from the plane, he will fly in the same direction as the plane, parallel to OxOx axis, covering a unit of distance every second. Naturally, he will also descend; thus his second coordinate will decrease by one unit every second.

There are ascending air flows on certain segments, each such segment is characterized by two numbers x1x1 and x2x2 (x1<x2x1<x2) representing its endpoints. No two segments share any common points. When the glider is inside one of such segments, he doesn't descend, so his second coordinate stays the same each second. The glider still flies along OxOx axis, covering one unit of distance every second.

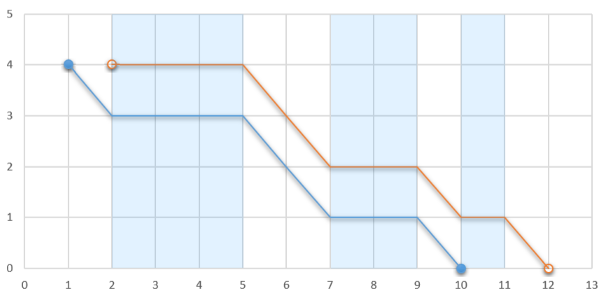If the glider jumps out at 11, he will stop at 1010. Otherwise, if he jumps out at 22, he will stop at 1212.

Determine the maximum distance along OxOx axis from the point where the glider's flight starts to the point where his flight ends if the glider can choose any integer coordinate to jump from the plane and start his flight. After touching the ground the glider stops altogether, so he cannot glide through an ascending airflow segment if his second coordinate is 0.

Input

The first line contains two integers nn and hh (1≤n≤2⋅105,1≤h≤109)(1≤n≤2⋅105,1≤h≤109) — the number of ascending air flow segments and the altitude at which the plane is flying, respectively.

Each of the next nn lines contains two integers xi1xi1 and xi2xi2 (1≤xi1<xi2≤109) — the endpoints of the ii-th ascending air flow segment. No two segments intersect, and they are given in ascending order.

Output

Print one integer — the maximum distance along OxOx axis that the glider can fly from the point where he jumps off the plane to the point where he lands if he can start his flight at any integer coordinate.

---

题目大意

二维坐标系里有一些蓝色区域和白色区域。在蓝色区域中飞行高度不会降低；在白色区域中飞行每个单位会降低一个单位。

请找出一条路径使得水平飞行距离最远。

题目分析

可以看成是这个东西：

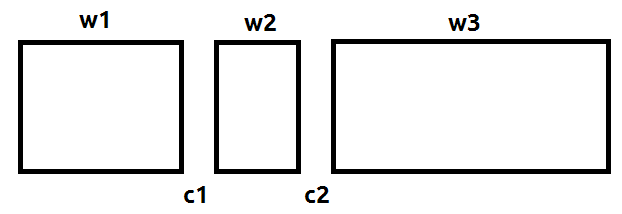
那么相当于是在选取的ci≤h的情况下，使Σwi最大。

于是做法还是挺显然的，因为对于每个起点，选取的[l,r]是单调的。

关键在于边界条件的小细节……今天做的时候WA了两发。

 #include<bits/stdc++.h>
 const int maxn = ;

 int n,h,l,r,lim,ans,cnt;
 int ls[maxn],rs[maxn];
 int w[maxn],c[maxn];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int main()
 {
     n = read(), h = read();
     for (int i=; i<=n; i++) ls[i] = read(), rs[i] = read();
     for (int i=; i<=n; i++)
         w[i] = rs[i]-ls[i], c[i] = ls[i+]-rs[i];
     r = , cnt = ans = w[];
     for (int i=; i<=n; i++)
     {
         while (r<n&&lim+c[r]<h) lim += c[r++], cnt += w[r];
         ans = std::max(ans, cnt);
         if (r!=i) lim -= c[i];　　　　　　　 //向前推一格
         else cnt += w[i+1], r = i+1;　　　　//间隙太大，置零重开
         cnt -= w[i];　　　　//减去当前位置
     }
     printf("%d\n",ans+h);
     return ;
 }

END