JZOJ 4213. 【五校联考1day2】对你的爱深不见底

题目

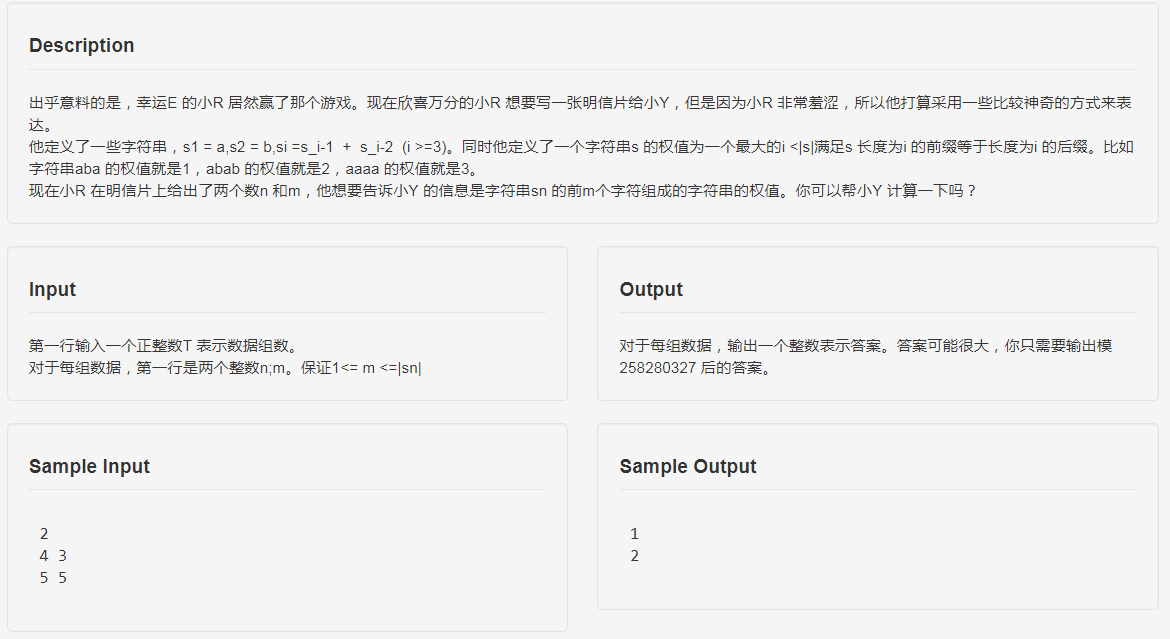
思路

结论题，我不会证明：

找到第一个 \(|S_n| \leq m + 1\)，那么答案就是 \(m - |S_{n-2}|\)

证明？我说了我不会，就当结论用吧

这已经很恶心了

然而这题还要打高精度？！

斐波那契数列太大了

注意有很多细节问题

就当留个高精度的优美板子吧！

\(Code\)

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
typedef long long LL;

const LL P = 258280327;
char s[1005];
int mm[1005] , f[5010][1005];
LL mo[5010];

inline void Plus(int a , int b , int c)
{
	int g = 0;
	f[c][0] = max(f[a][0] , f[b][0]);
	for(register int i = 1; i <= f[c][0]; i++)
	{
		f[c][i] = f[a][i] + f[b][i] + g;
		g = f[c][i] / 10;
		f[c][i] %= 10;
	}
	if (g) f[c][++f[c][0]] = g;
} 

inline bool check(int x)
{
	if (mm[0] < f[x][0]) return 1;
	if (mm[0] > f[x][0]) return 0;
	for(register int i = mm[0]; i; i--)
	if (mm[i] < f[x][i]) return 1;
	else if (mm[i] > f[x][i]) return 0;
	return 0;
}

inline void print(int x)
{
	LL sum = 0;
	for(register int i = mm[0]; i; i--) sum = (sum * 10 % P + mm[i]) % P;
	printf("%lld\n" , ((sum - 1 - mo[x - 2]) % P + P) % P);
}

int main()
{
	f[1][f[1][0] = 1] = 1 , f[2][f[2][0] = 1] = 1 , mo[1] = mo[2] = 1;
	for(register int i = 3; i <= 5000; i++) Plus(i - 1 , i - 2 , i) , mo[i] = (mo[i - 1] + mo[i - 2]) % P;

	int T;
	scanf("%d" , &T);
	for(; T; T--)
	{
		int n , len;
		scanf("%d%s" , &n , s);
		memset(mm , 0 , sizeof mm);

		len = strlen(s);
		for(register int i = len - 1; i >= 0; i--) mm[++mm[0]] = s[i] - '0';
		int g = 1;
		for(register int i = 1; i <= mm[0]; i++)
			mm[i] += g , g = mm[i] / 10 , mm[i] %= 10;
		if (g) mm[++mm[0]] = g;

		for(register int i = 3; i <= 5000; i++)
		if (check(i)){print(i); break;}
	}
}