最大流应用(Maximum Flow Application)

1. 二分图匹配(Bipartite Matching)

1.1 匹配(Matching)

Def. Given an undirected graph \(G = (V, E)\), subset of edges \(M ⊆ E\) is a matching if each node appears in at most one edge in \(M\).

定义. 给定一个无向图\(G = (V, E)\), 如果一个边的集合\(M \subseteq E\)并且每个顶点最多只出现在一条\(M\)中的边中, 则称\(M\)是一个匹配.

Max matching problem. Given a graph \(G\), find a max-cardinality matching.

最大匹配问题. 给定一个无向图\(G\), 找到一个集合元素最多的匹配.

1.2 二分图匹配(Bipartite matching)

Def. A graph G is bipartite if the nodes can be partitioned into two subsets \(L\) and \(R\) such that every edge connects a node in \(L\) with a node in \(R\).

Bipartite matching problem. Given a bipartite graph \(G = (L ∪ R, E)\), find a max cardinality matching.

max-flow formulation. Create digraph \(G' = (L ∪ R ∪ \set{s, t}, E')\):

• Direct all edges from \(L\) to \(R\), and assign infinite (or unit) capacity.
• Add unit-capacity edges from \(s\) to each node in \(L\).
• Add unit-capacity edges from each node in \(R\) to \(t\).

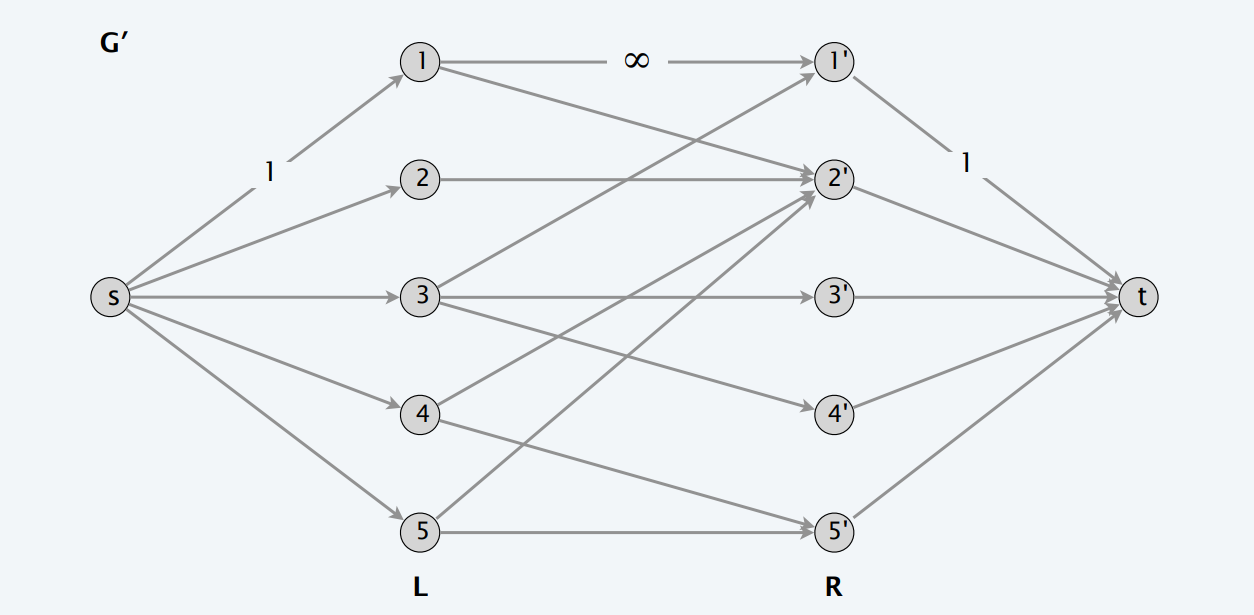
Theorem. 1–1 correspondence between matchings of cardinality \(k\) in \(G\) and integral flows of value \(k\) in \(G'\).

1.3 二分图完美匹配(Perfect matchings in bipartite graphs)

Def. Given a graph \(G = (V, E)\), a subset of edges \(M ⊆ E\) is a perfect matching if each node appears in exactly one edge in \(M\).

Notation. Let \(S\) be a subset of nodes, and let \(N(S)\) be the set of nodes adjacent to nodes in \(S\).

Observation. If a bipartite graph \(G = (L ∪ R, E)\) has a perfect matching, then \(|N(S)|\geq|S|\) for all subsets \(S \subseteq L\).

Theorem. [Frobenius 1917, Hall 1935] Let \(G = (L ∪ R, E)\) be a bipartite graph with \(|L| = |R|\). Then, graph G has a perfect matching iff \(|N(S)|\geq|S|\) for all subsets \(S \subseteq L\).

2. 不相交路径(Edge-disjoint Paths)

2.1 有向图中的不相交路径(Edge-disjoint Paths in Directed Graphs

2.1.1 问题描述(Problem Description)

Def. Two paths are edge-disjoint if they have no edge in common.

定义. 如果两个路径没有公共边, 则认为他们是不相交路径

Edge-disjoint paths problem. Given a digraph \(G = (V, E)\) and two nodes \(s\) and \(t\), find the max number of edge-disjoint \(s↝t\) paths.

不想交路径问题 给定一个有向图\(G = (V, E)\)和两个节点\(s\), \(t\), 找到其间不相交路径的最大数目.

2.1.2 解法(Solution)

Max-flow formulation. Assign unit capacity to every edge, and define it as \(G^\prime\)

Integral flow theorem. If each edge in a flow network has integral capacity, then there exists an integral maximal flow.

1–1 correspondence Theorem. 1–1 correspondence between k edge-disjoint \(s↝t\) paths in \(G\) and integral flows of value \(k\) in \(G'\).

• Integral flow theorem. \(\Rightarrow\) there exists a max flow \(f^*\) in \(G^\prime\) that is integral.
• 1–1 correspondence Theorem. \(\Rightarrow\) \(f^*\) corresponds to max number of edge-disjoint \(s↝t\) paths in \(G\).

2.1.3 补充(Addition)

Menger's Theorem. The max number of edge-disjoint \(s↝t\) paths equals the min number of edges whose removal disconnects \(t\) from \(s\).

2.2 无向图中的不相交路径(Edge-disjoint Paths in Undirected Graphs)

2.2.1 问题描述(Problem Description)

Given a graph \(G = (V, E)\) and two nodes \(s\) and \(t\), find the max number of edge-disjoint \(s↝t\) paths.

2.2.2 解法(Solution)

Max-flow formulation. Replace each edge with two antiparallel edges and assign unit capacity to every edge.

Observation. Two paths \(P1\) and \(P2\) may be edge-disjoint in the digraph but not edge-disjoint in the undirected graph

Lemma. In any flow network, there exists a maximum flow \(f\) in which for each pair of antiparallel edges \(e\) and \(e'\) : either \(f(e) = 0\) or \(f (e') = 0\) or both. Moreover, integrality theorem still holds.

Theorem. Max number of edge-disjoint \(s↝t\) paths = value of max flow.

3. 最大流问题扩展(Extensions to Max Flow)

3.1 多源点多汇点(Multiple sources and sinks)

Def. Given a digraph \(G = (V, E)\) with edge capacities \(c(e) ≥ 0\) and multiple source nodes and multiple sink nodes, find max flow that can be sent from the source nodes to the sink nodes.

max-flow formulation. Define new digraph as \(G'\):

• Add a new source node \(s\) and sink node \(t\).
• For each original source node \(s_i\) add edge \((s, s_i)\) with capacity \(\infty\).
• For each original sink node \(t_j\), add edge \((t_j, t)\) with capacity \(\infty\).

Claim. 1–1 correspondence between flows in \(G\) and \(G'\).

3.2 循环(Circulation)

3.2.1 供给需求循环(Circulation with supplies and demands)

Def. Given a digraph \(G = (V, E)\) with edge capacities \(c(e) ≥ 0\) and node demands \(d(v)\), a circulation is a function \(f(e)\) that satisfies:

• For each \(e\in E\): \(0\leq f(e)\leq c(e)\)
• For each \(v\in V\): \(\textstyle \sum_{e \space in \space to \space v}f(e) - \sum_{e \space out \space of \space v}f(e)=d(v)\)

max-flow formulation. Define new digraph as \(G'\):

• Add new source \(s\) and sink \(t\).
• For each \(v\) with \(d(v) < 0\), add \(edge (s, v)\) with capacity \(−d(v)\).
• For each \(v\) with \(d(v) > 0\), add \(edge (v, t)\) with capacity \(d(v)\).

Claim. \(G\) has circulation iff \(G'\) has max flow of value \(\displaystyle D = \sum_{v:d(v)>0}d(v) = \sum_{v:d(v)<0}-d(v)\)

3.2.2 带下界的供给需求循环(Circulation with supplies, demands, and lower bounds

Def. Given a digraph \(G = (V, E)\) with edge capacities \(c(e) ≥ 0\), lower bounds ℓ(e) ≥ 0, and node demands \(d(v)\), a circulation is a function \(f(e)\) that satisfies:

• For each \(e\in E\): \(\mathscr l(e)\leq f(e)\leq c(e)\)
• For each \(v\in V\): \(\textstyle \sum_{\text{e in to v}}f(e) - \sum_{\text{e out of v}}f(e)=d(v)\)

Max-flow formulation. Model lower bounds as circulation with demands.

Theorem. There exists a circulation in \(G\) iff there exists a circulation in \(G'\).

Moreover, if all demands, capacities, and lower bounds in \(G\) are integers, then there exists a circulation in \(G\) that is integer-valued.

4. 调查设计问题(Survey Design)

4.1 问题描述(Problem Description)

• Design survey asking \(n_1\) consumers about \(n_2\) products.
• Can survey consumer \(i\) about product \(j\) only if they own it.
• Ask consumer \(i\) between \(c_i\) and \(c_i'\) questions.
• Ask between \(p_j\) and \(p_j'\) consumers about product \(j\).

Goal. Design a survey that meets these specs, if possible.

4.2 解法(Solution)

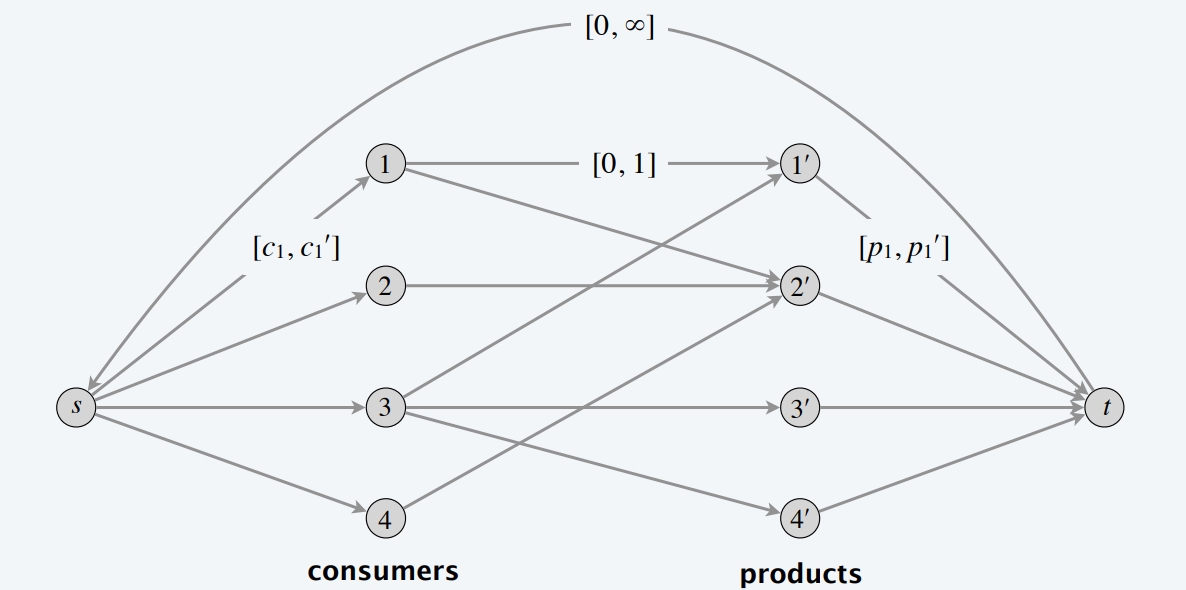
Max-flow formulation. Model as a circulation problem with lower bounds (all supplies and demands are 0):

• Add edge \((i, j)\) if consumer \(i\) owns product \(j\).
• Add edge from s to consumer \(j\).
• Add edge from product \(i\) to \(t\).
• Add edge from \(t\) to \(s\).
• All demands = 0.

Integer circulation \(\Leftrightarrow\) feasible survey design.