《Shader入门精要》中MVP变换的Projection矩阵与《GAMES101图形学入门》中的区别
game101的透视投影的投影矩阵是这样的

正交投影是这样的
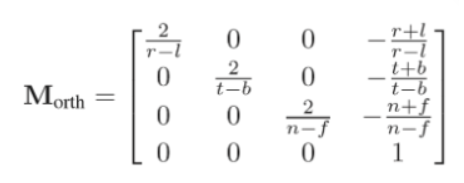
而shader入门精要的透视投影矩阵是这样子

正交投影矩阵是这样子
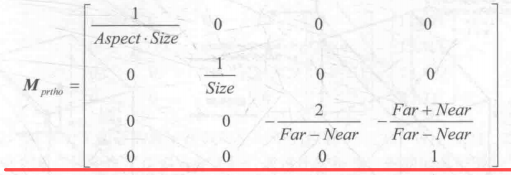
game101的透视投影是这样得到的

而正交投影的时候并没有假设中心点在面的中心

所以区别在于正交投影的时候有没有进行一步位移操作。
可能引起误导的地方
书上投影矩阵这样表示

而101则是认为转换成了正方体,但其实他的w是z,所以按照书上的来看,他也还没有进行归一化。
矩阵最后一行的1乘上z就会导致w变为z。看推导过程也能知道


再来看入门精要。

除了w之后,就当成是一个正方体了。
结论
所以两个在不考虑位移的情况下转换的效果是一样的,都是转换相机坐标得到准备归一化但是还没有归一化的坐标!只是书上画了锥体,games101画的是标准正方体。
《Shader入门精要》中MVP变换的Projection矩阵与《GAMES101图形学入门》中的区别的更多相关文章
- (转)思考:矩阵及变换,以及矩阵在DirectX和OpenGL中的运用问题:左乘/右乘,行优先/列优先,...
转自:http://www.cnblogs.com/soroman/archive/2008/03/21/1115571.html 思考:矩阵及变换,以及矩阵在DirectX和OpenGL中的运用1. ...
- 【c语言】二维数组中的查找,杨氏矩阵在一个二维数组中,每行都依照从左到右的递增的顺序排序,输入这种一个数组和一个数,推断数组中是否包括这个数
// 二维数组中的查找,杨氏矩阵在一个二维数组中.每行都依照从左到右的递增的顺序排序. // 每列都依照从上到下递增的顺序排序.请完毕一个函数,输入这种一个数组和一个数.推断数组中是否包括这个数 #i ...
- 《Shader入门精要》第11章-11.3.1流动的河流中的offset.x的解释
在我学习入门精要的时候,经常遇到不解释api,甚至是关键代码的实现原理. 11.3.1流动的河流中的offset.x的sin函数查了一下好像大家也都是书上原话直接复制,现在好不容易想明白了希望能帮到和 ...
- 【C语言】二维数组中的查找,杨氏矩阵
//二维数组中的查找,杨氏矩阵 //在一个二维数组中,每行都依照从左到右的递增的顺序排序.每列都依照从上到下递增的顺序排序. //请完毕一个函数.输入这种一个数组和一个数,推断数组中是否包括这个数. ...
- Unity Shader入门精要学习笔记 - 第16章 Unity中的渲染优化技术
转自冯乐乐的 <Unity Shader 入门精要> 移动平台的特点 为了尽可能一处那些隐藏的表面,减少overdraw(即一个像素被绘制多次),PowerVR芯片(通常用于ios设备和某 ...
- Unity Shader入门精要学习笔记 - 第6章 开始 Unity 中的基础光照
转自冯乐乐的<Unity Shader入门精要> 通常来讲,我们要模拟真实的光照环境来生成一张图像,需要考虑3种物理现象. 首先,光线从光源中被发射出来. 然后,光线和场景中的一些物体相交 ...
- Unity Shader入门精要读书笔记(一)序章
本系列的博文是笔者读<Unity Shader入门精要>的读书笔记,这本书的章节框架是: 第一章:着手准备. 第二章:GPU流水线. 第三章:Shader基本语法. 第四章:Shader数 ...
- Unity Shader入门精要学习笔记 - 第11章 让画面动起来
转自 冯乐乐的 <Unity Shader入门精要> Unity Shader 中的内置变量 动画效果往往都是把时间添加到一些变量的计算中,以便在时间变化时画面也可以随之变化.Unity ...
- Unity Shader入门精要学习笔记 - 第9章 更复杂的光照
转载自 冯乐乐的<Unity Shader入门精要> Unity 的渲染路径 在Unity里,渲染路径决定了光照是如何应该到Unity Shader 中的.因此,如果要和光源打交道,我们需 ...
随机推荐
- linux安装python3.6.6和新建虚拟环境
基础准备 修改本地时区 cp -rf /usr/share/zoneinfo/Asia/Shanghai /etc/localtime 安装epel yum源 yum -y install epel- ...
- Foundation框架介绍
1.Foundation框架介绍 什么是框架? 众多功能\API的集合 框架是由许多类.方法.函数.文档按照一定的逻辑组织起来的集合,以便使研发程序变得更容易,在OS X下的Mac操作系统中大约有80 ...
- Redis主从复制、读写分离
一.Redis的主从复制是什么 主机数据更新后根据配置和策略,自行同步到备机的master/slave机制,Master以写为主,Slave以读为主. 二.Redis的主从复制能干什么 读写分离 容灾 ...
- 测试前期API未实现时,如何写测试方法
大家在做接口测试的时候可能经历过这种情况,开发出来接口文档后,测试人员就要开始编写接口测试的自动化代码.这时就会用到了mock server,mock server不在这里说了,百度一大堆,想怎么实现 ...
- Go语言程序调试
1. Go语言二进制程序分析 在分析一些使用GOlang语言进行编译的恶意程序时,由于程序在被打包成二进制程序时会打包诸多引用的库,并且作者对二进制程序进行了去符号化,导致在动态或是静态分析时函 ...
- Java线程的实现/创建方式
1.继承Thread类: Thread 类本质上是实现了 Runnable 接口的一个实例,代表一个线程的实例. 启动线程的唯一方法就是通过 Thread 类的 start()实例方法. start( ...
- Spring容器变化之SmartLifecycle,LifecycleProcesso接口详述
Spring Boot run方法启动后相应的服务也随之启动,这个操作很妙.使用者都不用关心什么服务怎么启动,不管多少个服务怎么启动只要符合Spring Boot的启动规则都可以使用其run方法同一启 ...
- 使用java程序完成大量文件目录拷贝工作
java程序完成目录拷贝工作 背景描述:我目录有140多个,每个目录里面都有一个src目录.我现在想要所有的src目录移动到同一个目录中. package com.util.cp; import ja ...
- ARM7、ARM9、ARM11、ARM-Cortex系列的关系
参考资料: https://zhuanlan.zhihu.com/p/92315825 https://zhuanlan.zhihu.com/p/82337495 ARM是Advanced RISC ...
- 施耐德NOE77101后门漏洞分析
固件下载地址: GitHub - ameng929/NOE77101_Firmware 文件目录结构,这里只列出了一些主要的文件信息: ├── bin ├── ftp ├── fw ├── rdt ├ ...
