Neural Network模型复杂度之Batch Normalization - Python实现

• 背景介绍
  
  Neural Network之模型复杂度主要取决于优化参数个数与参数变化范围. 优化参数个数可手动调节, 参数变化范围可通过正则化技术加以限制. 本文从参数变化范围出发, 以Batch Normalization技术为例, 简要演示Batch Normalization批归一化对Neural Network模型复杂度的影响.

• 算法特征
  
  ①. 重整批特征之均值与方差; ②. 以批特征均值与方差之凸组合估计整体特征均值与方差

• 算法推导
  
  以批数据集\(X_B = \{x^{(1)}, x^{(2)}, \cdots, x^{(n)}\}\)为例, 重整前均值与标准偏差分别如下

  \[\begin{align*}
  \mu_B &= \frac{1}{n}\sum_i x^{(i)} \\
  \sigma_B &= \sqrt{\frac{1}{n}\sum_i (x^{(i)} - \mu_B)^2 + \epsilon}
  \end{align*}
  \]

  其中, \(\epsilon\)代表足够小正数, 确保标准偏差非零.
  
  对此批数据集进行如下重整,

  \[x_{\mathrm{new}}^{(i)} = \sigma_{B, \mathrm{new}}\frac{x^{(i)} - \mu_B}{\sigma_B} + \mu_{B, \mathrm{new}}
  \]

  其中, \(\mu_{B,\mathrm{new}}\)与\(\sigma_{B, \mathrm{new}}\)为待优化参数, 分别代表批数据集重整后均值与标准偏差. 以此手段构建线性层, 重置了数据特征之分布范围, 调整了模型复杂度.
  
  在训练过程中, 采用如下凸组合估计整体特征重整前均值与标准偏差,

  \[\begin{align*}
  \mu &= \lambda\mu + (1 - \lambda)\mu_{B} \\
  \sigma &= \lambda\sigma + (1-\lambda)\sigma_{B}
  \end{align*}
  \]

  其中, \(\lambda\)代表权重参数. 在测试过程中, 此\(\mu\)与\(\sigma\)用于替代\(\mu_B\)与\(\sigma_B\).

• 数据、模型与损失函数
  
  此处采用与Neural Network模型复杂度之Dropout - Python实现相同的数据、模型与损失函数, 并在隐藏层取激活函数tanh之前引入Batch Normalization层.

• 代码实现
  
  本文拟将中间隐藏层节点数设置为300, 使模型具备较高复杂度. 通过添加Batch Normalization层与否, 观察Batch Normalization对模型收敛的影响.

  code

  import numpy
  import torch
  from torch import nn
  from torch import optim
  from torch.utils import data
  from matplotlib import pyplot as plt
  
  numpy.random.seed(0)
  torch.random.manual_seed(0)
  
  # 获取数据与封装数据
  def xFunc(r, g, b):
      x = r + 2 * g + 3 * b
      return x
  
  def yFunc(r, g, b):
      y = r ** 2 + 2 * g ** 2 + 3 * b ** 2
      return y
  
  def lvFunc(r, g, b):
      lv = -3 * r - 4 * g - 5 * b
      return lv
  
  class GeneDataset(data.Dataset):
  
      def __init__(self, rRange=[-1, 1], gRange=[-1, 1], bRange=[-1, 1], num=100,\
                  transform=None, target_transform=None):
          self.__rRange = rRange
          self.__gRange = gRange
          self.__bRange = bRange
          self.__num = num
          self.__transform = transform
          self.__target_transform = target_transform
  
          self.__X = self.__build_X()
          self.__Y_ = self.__build_Y_()
  
      def __build_X(self):
          rArr = numpy.random.uniform(*self.__rRange, (self.__num, 1))
          gArr = numpy.random.uniform(*self.__gRange, (self.__num, 1))
          bArr = numpy.random.uniform(*self.__bRange, (self.__num, 1))
          X = numpy.hstack((rArr, gArr, bArr))
          return X
  
      def __build_Y_(self):
          rArr = self.__X[:, 0:1]
          gArr = self.__X[:, 1:2]
          bArr = self.__X[:, 2:3]
          xArr = xFunc(rArr, gArr, bArr)
          yArr = yFunc(rArr, gArr, bArr)
          lvArr = lvFunc(rArr, gArr, bArr)
          Y_ = numpy.hstack((xArr, yArr, lvArr))
          return Y_
  
      def __len__(self):
          return self.__num
  
      def __getitem__(self, idx):
          x = self.__X[idx]
          y_ = self.__Y_[idx]
          if self.__transform:
              x = self.__transform(x)
          if self.__target_transform:
              y_ = self.__target_transform(y_)
          return x, y_
  
  # 构建模型
  class Linear(nn.Module):
  
      def __init__(self, in_features, out_features, bias=True):
          super(Linear, self).__init__()
  
          self.__in_features = in_features
          self.__out_features = out_features
          self.__bias = bias
  
          self.weight = nn.Parameter(torch.randn((in_features, out_features), dtype=torch.float64))
          self.bias = nn.Parameter(torch.randn((out_features,), dtype=torch.float64))
  
      def forward(self, X):
          X = torch.matmul(X, self.weight)
          if self.__bias:
              X += self.bias
          return X
  
  class Tanh(nn.Module):
  
      def __init__(self):
          super(Tanh, self).__init__()
  
      def forward(self, X):
          X = torch.tanh(X)
          return X
  
  class BatchNorm(nn.Module):
  
      def __init__(self, num_features, lamda=0.9, epsilon=1.e-6):
          super(BatchNorm, self).__init__()
  
          self.__num_features = num_features
          self.__lamda = lamda
          self.__epsilon = epsilon
          self.training = True
  
          self.__mu_new = nn.parameter.Parameter(torch.zeros((num_features,)))
          self.__sigma_new = nn.parameter.Parameter(torch.ones((num_features,)))
          self.__mu = torch.zeros((num_features,))
          self.__sigma = torch.ones((num_features,))
  
      def forward(self, X):
          if self.training:
              mu_B = torch.mean(X, axis=0)
              sigma_B = torch.sqrt(torch.var(X, axis=0) + self.__epsilon)
              X = (X - mu_B) / sigma_B
              X = X * self.__sigma_new + self.__mu_new
  
              self.__mu = self.__lamda * self.__mu + (1 - self.__lamda) * mu_B.data
              self.__sigma = self.__lamda * self.__sigma + (1 - self.__lamda) * sigma_B.data
              return X
          else:
              X = (X - self.__mu) / self.__sigma
              X = X * self.__sigma_new + self.__mu_new
              return X
  
  class MLP(nn.Module):
  
      def __init__(self, hidden_features=50, is_batch_norm=True):
          super(MLP, self).__init__()
  
          self.__hidden_features = hidden_features
          self.__is_batch_norm = is_batch_norm
          self.__in_features = 3
          self.__out_features = 3
  
          self.lin1 = Linear(self.__in_features, self.__hidden_features)
          if self.__is_batch_norm:
              self.bn1 = BatchNorm(self.__hidden_features)
          self.tanh = Tanh()
          self.lin2 = Linear(self.__hidden_features, self.__out_features)
  
      def forward(self, X):
          X = self.lin1(X)
          if self.__is_batch_norm:
              X = self.bn1(X)
          X = self.tanh(X)
          X = self.lin2(X)
          return X
  
  # 构建损失函数
  class MSE(nn.Module):
  
      def forward(self, Y, Y_):
          loss = torch.sum((Y - Y_) ** 2)
          return loss
  
  # 训练单元与测试单元
  def train_epoch(trainLoader, model, loss_fn, optimizer):
      model.train(True)
  
      loss = 0
      with torch.enable_grad():
          for X, Y_ in trainLoader:
              optimizer.zero_grad()
  
              Y = model(X)
              lossVal = loss_fn(Y, Y_)
              lossVal.backward()
              optimizer.step()
  
              loss += lossVal.item()
      loss /= len(trainLoader.dataset)
      return loss
  
  def test_epoch(testLoader, model, loss_fn):
      model.train(False)
  
      loss = 0
      with torch.no_grad():
          for X, Y_ in testLoader:
              Y = model(X)
              lossVal = loss_fn(Y, Y_)
              loss += lossVal.item()
      loss /= len(testLoader.dataset)
      return loss
  
  # 进行训练与测试
  class BatchNormShow(object):
  
      def __init__(self, trainLoader, testLoader):
          self.__trainLoader = trainLoader
          self.__testLoader = testLoader
  
      def train(self, epochs=100):
          torch.random.manual_seed(0)
          model_BN = MLP(300, True)
          loss_BN = MSE()
          optimizer_BN = optim.Adam(model_BN.parameters(), 0.001)
  
          torch.random.manual_seed(0)
          model_NoBN = MLP(300, False)
          loss_NoBN = MSE()
          optimizer_NoBN = optim.Adam(model_NoBN.parameters(), 0.001)
  
          trainLoss_BN, testLoss_BN = self.__train_model(self.__trainLoader, self.__testLoader, \
              model_BN, loss_BN, optimizer_BN, epochs)
          trainLoss_NoBN, testLoss_NoBN = self.__train_model(self.__trainLoader, self.__testLoader, \
              model_NoBN, loss_NoBN, optimizer_NoBN, epochs)
  
          fig = plt.figure(figsize=(5, 4))
          ax1 = fig.add_subplot()
          ax1.plot(range(epochs), trainLoss_BN, "r-", lw=1, label="train with BN")
          ax1.plot(range(epochs), testLoss_BN, "r--", lw=1, label="test with BN")
          ax1.plot(range(epochs), trainLoss_NoBN, "b-", lw=1, label="train without BN")
          ax1.plot(range(epochs), testLoss_NoBN, "b--", lw=1, label="test without BN")
          ax1.legend()
          ax1.set(xlabel="epoch", ylabel="loss", yscale="log")
          fig.tight_layout()
          fig.savefig("batch_norm.png", dpi=100)
          plt.show()
  
      def __train_model(self, trainLoader, testLoader, model, loss_fn, optimizer, epochs):
          trainLossList = list()
          testLossList = list()
  
          for epoch in range(epochs):
              trainLoss = train_epoch(trainLoader, model, loss_fn, optimizer)
              testLoss = test_epoch(testLoader, model, loss_fn)
              trainLossList.append(trainLoss)
              testLossList.append(testLoss)
              print(epoch, trainLoss, testLoss)
          return trainLossList, testLossList
  
  if __name__ == "__main__":
      trainData = GeneDataset([-1, 1], [-1, 1], [-1, 1], num=1000, \
          transform=torch.tensor, target_transform=torch.tensor)
      testData = GeneDataset([-1, 1], [-1, 1], [-1, 1], num=300, \
          transform=torch.tensor, target_transform=torch.tensor)
      trainLoader = data.DataLoader(trainData, batch_size=len(trainData), shuffle=False)
      testLoader = data.DataLoader(testData, batch_size=len(testData), shuffle=False)
      bnsObj = BatchNormShow(trainLoader, testLoader)
      epochs = 10000
      bnsObj.train(epochs)
  

• 结果展示

  

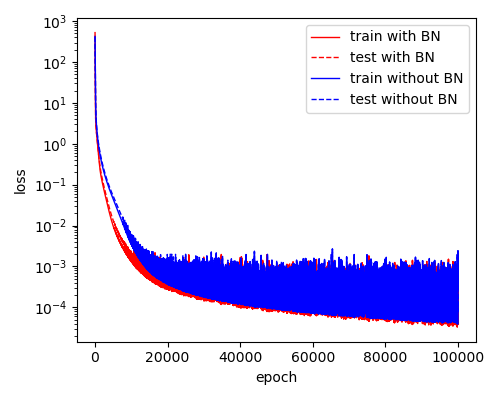
  可以看到, Batch Normalization使得模型具备更快的收敛速度, 不过对最终收敛值影响不大, 即在上述重整手段下模型复杂度变化不大.

• 使用建议
  
  ①. Batch Normalization改变了特征分布, 具备调整模型复杂度的能力;
  
  ②. Batch Normalization使特征分布在原点附近, 不容易出现梯度消失或梯度爆炸;
  
  ③. Batch Normalization适用于神经网络全连接层与卷积层.

• 参考文档
  
  ①. 动手学深度学习 - 李牧