Python数据分析I

Python数据分析概述

数据分析的含义与目标

统计分析方法

提取有用信息

研究、概括、总结

Python与数据分析

Python: Guido Van Rossum Christmas Holiday, 1989

特点：简介 开发效率搞 运算速度慢（相对于C++和Java） 胶水特性（集成C语言）

数据分析：numpy、scipy、matplotlib、pandas、scikit-learn、keras

Python数据分析大家族

numpy（Numeric Python）: 数据结构基础。是Python的一种开源的数值计算扩展。这种工具可用来存储和处理大型矩阵，比Python自身的嵌套列表（nested list structure)结构要高效的多（该结构也可以用来表示矩阵（matrix））。据说NumPy将Python相当于变成一种免费的更强大的MatLab系统。

scipy: 强大的科学计算方法（矩阵分析、信号和图像分析、数理分析……）

matplotlib: 丰富的可视化套件

pandas: 基础数据分析套件。该工具是为了解决数据分析任务而创建的。Pandas 纳入了大量库和一些标准的数据模型，提供了高效地操作大型数据集所需的工具。pandas提供了大量能使我们快速便捷地处理数据的函数和方法。Pandas最初被作为金融数据分析工具而开发出来，因此，pandas为时间序列分析提供了很好的支持。 Pandas的名称来自于面板数据（panel data）和python数据分析（data analysis）。

scikit-learn: 强大的数据分析建模库

keras: （深度）人工神经网络

Python环境搭建

平台：Windows、Linux、MacOS

科学计算工具：Anaconda

Python数据分析基础技术

I. numpy

关键词： 开源 数据计算扩展

功能： ndarray 多维操作 线性代数

ndarray

#encoding=utf-8
import numpy as np
def main():
    lst=[[1,2,3],[2,4,6]]
    print(type(lst))
    np_lst=np.array(lst)
    print(type(lst))
    np_lst=np.array(lst,dtype=np.float)
	# bool
	# int,int8,int16,int32,int64,int128
	# uint8,uint16,uint32,uint64,uint128,
	# float16/32/64,complex64/128
    print(np_lst.shape)			# 行列数
    print(np_lst.ndim)			# 维数
    print(np_lst.dtype)  		# 数据类型
    print(np_lst.itemsize)  	# 每个数据的数据存储大小
    print(np_lst.size)  		# 元素个数

some kinds of array

#encoding=utf-8
import numpy as np
def main():
    print(np.zeros([2, 4]))
    print(np.ones([3, 5]))
    print("Rand:")
    print(np.random.rand())                 # 0-1内均匀分布随机数
    print(np.random.rand(2, 4))
    print("RandInt:")
    print(np.random.randint(1, 10, 3))      # 3个1-10内随机分布整数
    print("Randn:")
    print(np.random.randn(2, 4))            # 标准正态随机数
    print("Choice:")
    print(np.random.choice([10, 20, 30]))   # 指定范围内的随机数
    print("Distribute:")
    print(np.random.beta(1, 10, 100))       # 比如Beta分布，Dirichlet分布etc

opeartion

#encoding=utf-8
import numpy as np
def main():
    print(np.arange(1, 11).reshape([2, 5]))
    lst = np.arange(1, 11).reshape([2, 5])
    print("Exp:")
    print(np.exp(lst))
    print("Exp2:")
    print(np.exp2(lst))
    print("Sqrt:")
    print(np.sqrt(lst))
    print("Sin:")
    print(np.sin(lst))
    print("Log:")
    print(np.log(lst))
    lst = np.array([[[1, 2, 3, 4],
                     [4, 5, 6, 7]],
                    [[7, 8, 9, 10],
                     [10, 11, 12, 13]],
                    [[14, 15, 16, 17],
                     [18, 19, 20, 21]]
                    ])
    print(lst)
    print("Sum:")
    print(lst.sum())            # 所有元素求和
    print(lst.sum(axis=0))      # 最外层求和
    print(lst.sum(axis=1))      # 第二层求和
    print(lst.sum(axis=-1))     # 最里层求和
    print("Max:")
    print(lst.max())
    print("Min:")
    print(lst.min())

    lst1 = np.array([10, 20, 30, 40])
    lst2 = np.array([4, 3, 2, 1])
    print("Add:")
    print(lst1 + lst2)
    print("Sub:")
    print(lst1 - lst2)
    print("Mul:")
    print(lst1 * lst2)
    print("Div:")
    print(lst1 / lst2)
    print("Square:")
    print(lst1 ** lst2)
    print("Dot:")
    print(np.dot(lst1.reshape([2, 2]), lst2.reshape([2, 2])))
    print("Cancatenate")
    print(np.concatenate((lst1, lst2), axis=0))
    print(np.vstack((lst1, lst2)))                  # 按照行拼接
    print(np.hstack((lst1, lst2)))                  # 按照列拼接
    print(np.split(lst1, 2))                        # 向量拆分
    print(np.copy(lst1))                            # 向量拷贝

liner algebra

#encoding=utf-8
import numpy as np
from numpy.linalg import *
def main():
    ## Liner
    print(np.eye(3))
    lst = np.array([[1, 2],
                    [3, 4]])
    print("Inv:")
    print(inv(lst))
    print("T:")
    print(lst.transpose())
    print("Det:")
    print(det(lst))
    print("Eig:")
    print(eig(lst))
    y = np.array([[5], [7]])
    print("Solve")
    print(solve(lst, y))

others

#encoding=utf-8
import numpy as np
def main():
    ## Other
    print("FFT:")
    print(np.fft.fft(np.array([1, 1, 1, 1, 1, 1, 1, 1, 1])))
    print("Coef:")
    print(np.corrcoef([1, 0, 1], [0, 2, 1]))
    print("Poly:")
    print(np.poly1d([2, 1, 3]))				#一元多次方程

II. matplotlib

关键词： 绘图库

Line

#encoding=utf-8
import numpy as np
import matplotlib.pyplot as plt

def Main():
    ## line
    x = np.linspace(-np.pi, np.pi, 256, endpoint=True)
    c, s = np.cos(x), np.sin(x)
    plt.plot(x, c)
    plt.figure(1)
    plt.plot(x, c, color="blue", linewidth=1.5, linestyle="-", label="COS", alpha=0.6)
    plt.plot(x, s, "r*", label="SIN", alpha=0.6)
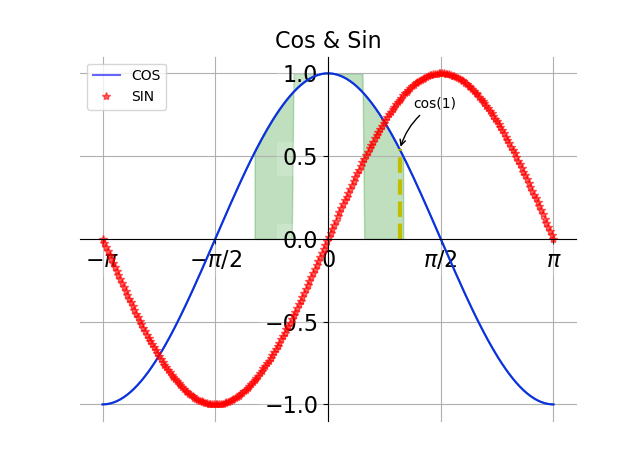
    plt.title("Cos & Sin", size=16)
    ax = plt.gca()                # 轴编辑器
    ax.spines["right"].set_color("none")
    ax.spines["top"].set_color("none")
    ax.spines["left"].set_position(("data", 0))
    ax.spines["bottom"].set_position(("data", 0))
    ax.xaxis.set_ticks_position("bottom")
    ax.yaxis.set_ticks_position("left")
    plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$\pi/2$', r'$\pi$']) 					# 正则表达
    plt.yticks(np.linspace(-1, 1, 5, endpoint=True))
    for label in ax.get_xticklabels()+ax.get_yticklabels():
        label.set_fontsize(16)
        label.set_bbox(dict(facecolor="white", edgecolor="none", alpha=0.2))
    plt.legend(loc="upper left")
    plt.grid()
    # plt.axis([-2, 1, -0.5, 1])
    # fill:填充
    plt.fill_between(x, np.abs(x) < 0.5, c, c > 0.5, color="green", alpha=0.25)
    t = 1
    plt.plot([t, t], [0, np.cos(t)], "y", linewidth=3, linestyle="--")
    plt.annotate("cos(1)", xy=(t, np.cos(1)), xycoords="data", xytext=(+10, +30),textcoords="offset points", arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

plt.fill_between(x, np.abs(x) < 0.5, c, c > 0.5, color="green", alpha=0.25)

第一个参数x表示x轴，第二个参数 np.abs(x)表示x的绝对值，np.abs(x) < 0.5是一个判定变量，c表示y轴，c > 0.5是一个判定条件。

当np.abs(x) < 0.5为真（1），从y轴的1（满足c>0.5）开始往两边填充（当然X轴上是-0.5到0.5之间的区域），此时填充的也就是图上方的两小块。当np.abs(x) >= 0.5为假（0），从y轴的0开始向上填充，当然只填充c>0.5的区域，也就是图中那两个大的对称区域。

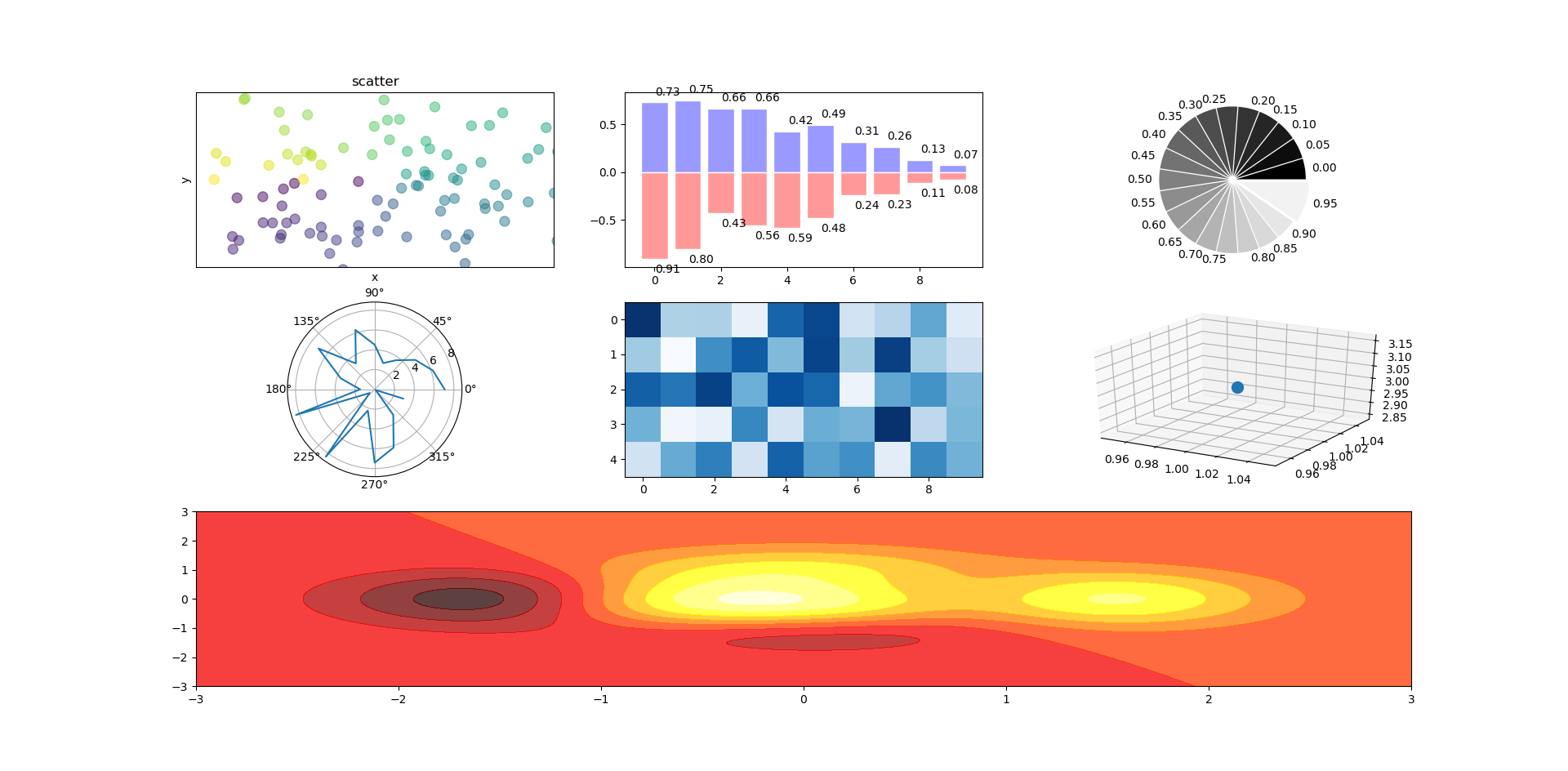
Many types of figures

#encoding=utf-8
import numpy as np
import matplotlib.pyplot as plt

def Main():
    fig = plt.figure()
    ## scatter
    ax = fig.add_subplot(3, 3, 1)
    n = 128
    X = np.random.normal(0, 1, n)
    Y = np.random.normal(0, 1, n)
    T = np.arctan2(Y, X)
    # plt.axes([0.025, 0.025, 0.95, 0.95])
    plt.scatter(X, Y, s=75, c=T, alpha=.5)
    plt.xlim(-1.5, 1.5), plt.xticks([])
    plt.ylim(-1.5, 1.5), plt.yticks([])
    plt.axis()
    plt.title("scatter")
    plt.xlabel("x")
    plt.ylabel("y")

    ## bar
    fig.add_subplot(332)
    n = 10
    X = np.arange(n)
    Y1 = (1 - X / float(n)) * np.random.uniform(0.5, 1, n)
    Y2 = (1 - X / float(n)) * np.random.uniform(0.5, 1, n)
    plt.bar(X, +Y1, facecolor='#9999ff', edgecolor='white')
    plt.bar(X, -Y2, facecolor='#ff9999', edgecolor='white')
    for x, y in zip(X,Y1):
        plt.text(x + 0.4, y + 0.05, '%.2f' % y, ha='center', va='bottom')
    for x, y in zip(X,Y2):
        plt.text(x + 0.4, - y - 0.05, '%.2f' % y, ha='center', va='top')

    ## Pie
    fig.add_subplot(333)
    n = 20
    Z = np.ones(n)
    Z[-1] *= 2
    # explode扇形离中心距离
    plt.pie(Z, explode=Z*.05, colors=['%f' % (i / float(n)) for i in range(n)],
            labels=['%.2f' % (i / float(n)) for i in range(n)])
    plt.gca().set_aspect('equal')       # 圆形
    plt.xticks([]), plt.yticks([])

    ## polar
    fig.add_subplot(334, polar=True)
    n = 20
    theta = np.arange(0, 2 * np.pi, 2 * np.pi / n)
    radii = 10 * np.random.rand(n)
    plt.polar(theta, radii)
    # plt.plot(theta, radii)

    ## heatmap
    fig.add_subplot(335)
    from matplotlib import cm
    data = np.random.rand(5, 10)
    cmap = cm.Blues
    map = plt.imshow(data, interpolation='nearest', cmap=cmap, aspect='auto', vmin=0, vmax=1)

    ## 3D
    from mpl_toolkits.mplot3d import Axes3D
    ax = fig.add_subplot(336, projection="3d")
    ax.scatter(1, 1, 3, s=100)

    ## hot map
    fig.add_subplot(313)
    def f(x, y):
        return (1 - x / 2 + x ** 5 + y ** 3) * np.exp(- x ** 2 - y ** 2)
    n = 256
    x = np.linspace(-3, 3, n * 2)
    y = np.linspace(-3, 3, n)
    X, Y = np.meshgrid(x, y)
    plt.contourf(X, Y, f(X, Y), 8, alpha=.75, cmap=plt.cm.hot)
	plt.savefig("./data/fig.png")
    plt.show()