Bellman-Ford 最短路径算法

算法证明：http://courses.csail.mit.edu/6.006/spring11/lectures/lec15.pdf

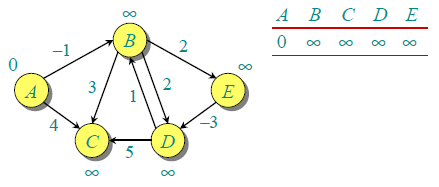
先来看一个这样的图：

这是含有负边权的，如果是用djistra的话将会进行无限次松弛操作。从这里可以看出松弛操作是有一点问题的，如果存在负环，将无止尽的松弛，最短路也就不存在了。还有就是选择不同的遍历顺序对于松弛操作来说是挺重要的。今天就来了解一下聪明的Bellman-Ford算法吧！

Bellman-Ford算法每一轮把边按照一定的顺序，逐条边进行松弛。经过|V|-1轮后，得到的必定是最短路径。

献上松弛操作和Bellman-Ford算法的伪代码：

/*
松弛操作
*/
for v in V:
    dist[v] = ∞
dist[s]=
while some edge(u,v) has dist[v]>dist[u]+w(u,v):
    pick such an edge(u,v)
    relax(u,v):
        if dist[v]>dist[u]+w(u,v):
            dist[v]=dist[u]+w(u,v)

/*
Bellman-Ford
*/
for v in V:
    dist[v] = ∞
dist[s]=
for i from  to |V|-:
    for(u,v)in E:
    relax(u,v):
        if dist[v]>dist[u]+w(u,v):
            dist[v]=dist[u]+w(u,v)

接下来就以上图为例，按照以下顺序处理所有的边：(A,B),(A,C),(B,C),(B,D),(B,E),(E,D),(D,B),(D,C).

然后进行第一次迭代：

最开始dist数组的内容为[0,∞，∞，∞，∞],现在处理(A,B),由于dist[B]=∞，dist[A]+w(A,B)=-1，此时应更新dist[B]，即dist为[0,-1，∞，∞，∞]。

同理，按照顺序逐个处理边，将得到以下的dist变化过程：

[0,-1，4，∞，∞]      (A,C)

[0,-1，2，∞，∞]　　(B,C)

[0,-1，2，1，∞]　　(B,D)

[0,-1，2，1，1]　　(B,E)

[0,-1，2，-2，1]　　(E,D)

[0,-1，2，-2，1]　　(D,B)

[0,-1，2，-2，1]　　(D,C)

第一轮的最后结果就为上面最后一行，当然了，这个不一定是最优的，因此我们还需要进行下一轮，经过|V-1|次后就一定能求出最短路了。

当然，存在负环是无法得到最短路的，此时只需要在最后进行判断，对每条边都判断以下能不能再进行松弛操作，如果存在可以的边，那就是出现负环了。