牛客小白月赛12 D 月月给华华出题 （欧拉函数，数论，线筛）

链接：https://ac.nowcoder.com/acm/contest/392/D

来源：牛客网

月月给华华出题

时间限制：C/C++ 2秒，其他语言4秒

空间限制：C/C++ 131072K，其他语言262144K

64bit IO Format: %lld

题目描述

因为月月是个信息学高手，所以她也给华华出了一题，让他求：

\sum_{i=1}^N\frac{i}{\gcd(i,N)}∑

i=1

N

​

gcd(i,N)

i

​

但是因为这个式子实在太简单了，所以月月希望华华对N=1,2,...,n各回答一次。华华一脸懵逼，所以还是决定把这个问题丢给你。

输入描述:

一个正整数n。

输出描述:

输出n行，第i行表示N=i时的答案。

示例1

输入

复制

6

输出

复制

1

2

4

6

11

11

备注:

1\le n\le 10^61≤n≤10

6

请注意输出的效率

思路：

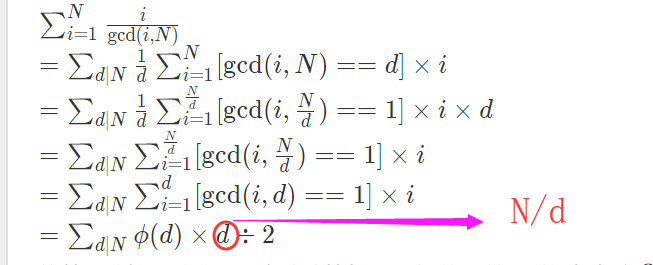
最后一步是根据这个欧拉函数的一个得出的：

小于等于n的数中与n互质的数sum和为phi(n) * n/2

phi（x）为欧拉函数

由于题目要求输出1~n的每一个答案，那么我们从1到n枚举i当做上式中因子d来计算对每个答案的贡献即可。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
ll phi[maxn];
ll prime[maxn];
int check[maxn];
int tot = 0;
void build_phi()
{
    phi[1] = 1ll;
    memset(check, 0, sizeof(check));
    for (int i = 2; i < 1000010; ++i)
    {
        if (!check[i])
        {
            prime[tot++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; j < tot; ++j)
        {
            if (i * prime[j] > 1000010)
            {
                break;
            }
            check[i * prime[j]] = 1;
            if (i % prime[j] == 0)
            {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            } else {
                phi[i * prime[j]] = phi[i] * (prime[j] - 1);
            }
        }
    }
}
ll ans[maxn];
int main()
{
    //freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);

    int n;
    scanf("%d", &n);
    build_phi();
    for (ll i = 1; i <= n; ++i)
    {
        for (ll j = i; j <= n; j += i)
        {
            ans[j] += phi[j / i] * (j / i) / 2ll;
        }
    }
    repd(i, 1, n)
    {
        printf("%lld\n", ans[i] + 1ll );
    }

    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}