leetcode-64. 最小路径和 · vector + DP

题面

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

给定二维数组，从（0， 0）开始，只能向右和向下走，找到最小的路径和。

样例

Input:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

思路

动态规划，打表。我们就模拟移动的路径。我们需要一个二维数组来存储每一步的路径值。

可以在原来二维数组基础上，直接进行操作。

第一排只能向右走得到；第一列只能向下走得到。

其他的就要参考它的上边元素值和左边元素值，取小在加上它本身，更新成为它。（因为要最小路径，所以我们要确保每一步都最小）

算法

1. 遍历第一行，当前元素值为它左边元素加上它本身（只能从左边向右边走）；

2. 遍历第一列，当前元素值为它上边元素加上它本身（只能从上边向下边走）；

3. 遍历二维数组其他元素，当前值为上边元素与左边元素最小值加上它本身；

4. 返回右下角元素，即是结果。

时间复杂度：O(n²)

空间复杂度：O(n²)

源码

 class Solution {
 public:
     int minPathSum(vector<vector<int>>& grid) {
         int row = grid.size(), col = grid[].size();
         if(row == )
             return ;
         for(int i=; i<col; i++)
         {
             grid[][i] += grid[][i-];
         }
         for(int i=; i<row; i++)
         {
             grid[i][] += grid[i-][];
         }
         for(int i=; i<row; i++)
         {
             for(int j=; j<col; j++)
             {
                 grid[i][j] += min(grid[i][j-], grid[i-][j]);
             }
         }
         return grid[row-][col-];
     }
 };

优化：空间压缩

其实，我们在做的过程当中，一直在做行处理，即一直在更新某一行（更新完这一行就转向下一行）。那么，我们只需要一个一维数组即可解决这个问题。

这样一来，空间就压缩到了O(n)，时间复杂度不变。

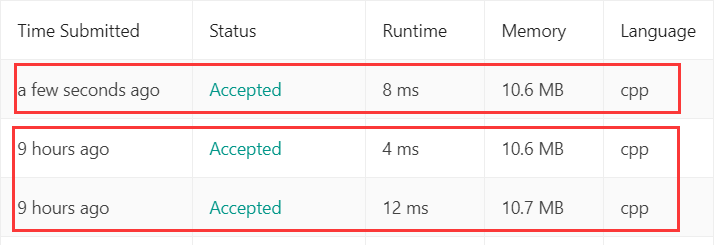
（1-压缩后的；2-压缩前的）似乎空间占用也没有多大变化，但是我们确实做了空间压缩。

空间压缩源码

只用一维数组在存储状态，就要重新推导一下更新的状态方程

第一行：dp[0] = grid[0][0]

　　　　dp[i] = grid[0][i] +  dp[i-1]

其他行：dp[0] = grid[i][0] + dp[0]

　　　　dp[j] = grid[i][j] +  min(dp[j-1], dp[j])

 int minPathSum(vector<vector<int>>& grid) {
         int row = grid.size(), col = grid[].size();
         if(row == )
             return ;
         vector<int> dp(col, );//只要额外一维数组的空间，上一种做法，如果不原地使用原来二位数组的话，就只能额外开二维数组。
         dp[] = grid[][];
         for(int i=; i<col; i++)
         {
             dp[i] = dp[i-] + grid[][i];
         }
         for(int i=; i<row; i++)
         {
             dp[] += grid[i][];
             for(int j=; j<col; j++)
             {
                 dp[j] = min(dp[j-], dp[j]) + grid[i][j];
             }
         }
         return dp[col-];
     }