cordic
cordic里向量旋转得到新向量,利用的是旋转矩阵
摘自百度百科维基百科
旋转矩阵(Rotation matrix)是在乘以一个向量的时候改变向量的方向但不改变大小的效果的矩阵。旋转矩阵不包括反演,它不可以把右手坐标系改变成左手坐标系或反之。所有旋转加上反演形成了正交矩阵的集合。对于3D坐标系,任意两个坐标系却不能等价。实际上,存在两种完全不同的3D坐标系:左手坐标系和右手坐标系。如果同属于左手坐标系或者右手坐标系,则可以通过旋转来重合,否则不可以

参考文献:
基于CORDIC 改进算法的反正切函数
在FPGA 中的实现
刘小会1,许蕾2,刘海颖2,王惠南1
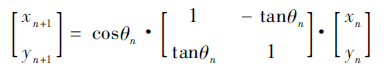
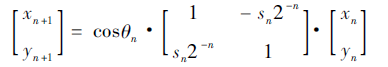

cordic的更多相关文章
- CORDIC原理与FPGA实现(2)
CORDIC算法实现极坐标(polar)到直角坐标系(Cartesian)的变换. 1: function [horizonal,vertical]=polar2car(mag, pha); 2: x ...
- CORDIC原理与FPGA实现(1)
CORDIC算法的来历与用途大家网上随处可以见到,这里写 一下自己的理解. 将P(x,y)旋转角度a得到新的坐标P’(x’,y’).这里的坐标变换为: x’= x cos(a) – y sin(a) ...
- 三角函数计算,Cordic 算法入门
[-] 三角函数计算Cordic 算法入门 从二分查找法说起 减少乘法运算 消除乘法运算 三角函数计算,Cordic 算法入门 三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来 ...
- (转)三角函数计算,Cordic 算法入门
由于最近要使用atan2函数,但是时间上消耗比较多,因而网上搜了一下简化的算法. 原帖地址:http://blog.csdn.net/liyuanbhu/article/details/8458769 ...
- 基于FPGA的cordic算法的verilog初步实现
最近在看cordic算法,由于还不会使用matlab,真是痛苦,一系列的笔算才大概明白了这个算法是怎么回事.于是尝试用verilog来实现.用verilog实现之前先参考软件的程序,于是先看了此博文h ...
- Cordic 算法之 反正切
在通信的算法中,常采用Cordic算法之一,知道角度产生正交的的正弦余弦, 或者知道正弦和余弦求角度,求反正切. 1. 求正弦和余弦值. 方法:旋转角度,得到正弦余弦值: 再旋转角度,到达下一个正弦余 ...
- Cordic 算法的原理介绍
cordic 算法知道正弦和余弦值,求反正切,即角度. 采用用不断的旋转求出对应的正弦余弦值,是一种近似求解发. 旋转的角度很讲求,每次旋转的角度必须使得 正切值近似等于 1/(2^N).旋转的目的是 ...
- Cordic算法——verilog实现
上两篇博文Cordic算法--圆周系统之旋转模式.Cordic算法--圆周系统之向量模式做了理论分析和实现,但是所用到的变量依然是浮点型,而cordic真正的用处是基于FPGA等只能处理定点的平台.只 ...
- Cordic算法——圆周系统之向量模式
旋转模式用来解决三角函数,实现极坐标到直角坐标的转换,基础理论请参考Cordic算法--圆周系统之旋转模式.那么,向量模式则用来解决反三角函数的问题,体现的应用主要是直角坐标向极坐标转换,即已知一点的 ...
- Cordic算法——圆周系统之旋转模式
三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来计算任意角度的三角函数的值.这种表格在人们刚刚产生三角函数的概念的时候就已经有了,它们通常是通过从已知值(比如sin(π/2)= ...
随机推荐
- Python将数据渲染到docx文档指定位置
超简单Python将指定数据插入到docx模板渲染并生成 最近有一个需求,制作劳动合同表,要从excel表格中将每个人的数据导入到docx劳动合同中,重复量很大,因此可以使用python高效解决.为了 ...
- linux 基础 用户操作
命令: 1. whoami 2.su 用户名 3.useradd 用户名 4.passwd 用户名
- C#连接数据库插入数据
首先是安装JDBC操作数据库的包,,当然自己看着办哈,可以自己下载以后导入,或者直接让软件本身下载 第一种方式 第二种 咱自己下载个低版本的 点击这个链接 点击以后呢可以直接下载下来,然后导入(大家百 ...
- Linux 小记 — Ubuntu 自动化配置
前言 工欲善其事,必先利其器.经过多次的重复配置 ubuntu 开发坏境,我终于决定花点时间总结一下,并将其写成一个自动化配置脚本.服务器实例:ubuntu 16.04,技术栈:shell,pytho ...
- Jenkins构建自动化任务
前言 Jenkins是一个开源软件项目,是基于Java开发的一种持续集成工具,用于监控持续重复的工作,旨在提供一个开放易用的软件平台,使软件的持续集成变成可能. 一.环境配置 1.切换到jenkins ...
- 第三次作业(1) Visual Studio程序安装过程和练习过程
Visual Studio程序安装过程和练习过程 第一步 首先要在网上找一个VS2013的安装包,之后我安装在D盘上,C盘上也需要有5.2G空间,勾选相应的选项,才能继续安装. 安装的过程很漫长,接近 ...
- M1m2分析报告
个人博客链接: http://www.cnblogs.com/kjzxzzh/p/4074386.html http://www.cnblogs.com/kjzxzzh/p/4027699.html ...
- M2项目测试
更为详细的测试报告,我们会在后续整理出来. 在M1的基础上,我们新增加了两个个数据表来存放问答对以及标签信息的表:C705question表 与 tag表 第二次迭代中,我们积极地同第三组沟通,了解到 ...
- 毕业设计 之 五 PHP语法学习笔记
毕业设计 之 四 PHP语法学习笔记 作者:20135216 平台:windows10 软件:XAMPP,DreamWeaver 说明:该笔记是对网站编程语言的详细学习 一.PHP基础 0. 关于环境 ...
- Linux实践三:程序破解
一.汇编指令机器码 二.反汇编与十六进制编程器 三.可执行文件的基本格式 hexdump -x login 用16进制数字显示login内容 objdump -x login 显示login中各个段以 ...
