神经网络优化篇：详解RMSprop

RMSprop

知道了动量（Momentum）可以加快梯度下降，还有一个叫做RMSprop的算法，全称是root mean square prop算法，它也可以加速梯度下降，来看看它是如何运作的。

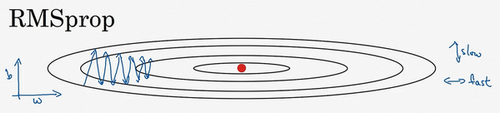
回忆一下之前的例子，如果执行梯度下降，虽然横轴方向正在推进，但纵轴方向会有大幅度摆动，为了分析这个例子，假设纵轴代表参数\(b\)，横轴代表参数\(W\)，可能有\(W_{1}\)，\(W_{2}\)或者其它重要的参数，为了便于理解，被称为\(b\)和\(W\)。

所以，想减缓\(b\)方向的学习，即纵轴方向，同时加快，至少不是减缓横轴方向的学习，RMSprop算法可以实现这一点。

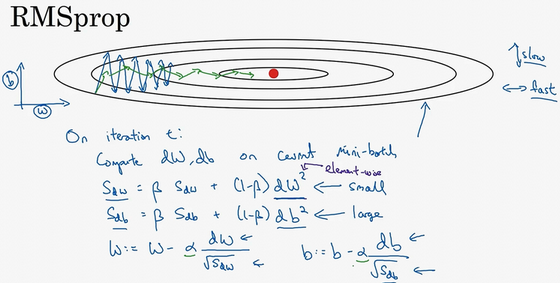
在第\(t\)次迭代中，该算法会照常计算当下mini-batch的微分\(dW\)，\(db\)，所以会保留这个指数加权平均数，用到新符号\(S_{dW}\)，而不是\(v_{dW}\)，因此\(S_{dW}= \beta S_{dW} + (1 -\beta) {dW}^{2}\)，澄清一下，这个平方的操作是针对这一整个符号的，这样做能够保留微分平方的加权平均数，同样\(S_{db}= \beta S_{db} + (1 - \beta){db}^{2}\)，再说一次，平方是针对整个符号的操作。

接着RMSprop会这样更新参数值，\(W:= W -a\frac{dW}{\sqrt{S_{dW}}}\)，\(b:=b -\alpha\frac{db}{\sqrt{S_{db}}}\)，来理解一下其原理。记得在横轴方向或者在例子中的\(W\)方向，希望学习速度快，而在垂直方向，也就是例子中的\(b\)方向，希望减缓纵轴上的摆动，所以有了\(S_{dW}\)和\(S_{db}\)，希望\(S_{dW}\)会相对较小，所以要除以一个较小的数，而希望\(S_{db}\)又较大，所以这里要除以较大的数字，这样就可以减缓纵轴上的变化。看这些微分，垂直方向的要比水平方向的大得多，所以斜率在\(b\)方向特别大，所以这些微分中，\(db\)较大，\(dW\)较小，因为函数的倾斜程度，在纵轴上，也就是b方向上要大于在横轴上，也就是\(W\)方向上。\(db\)的平方较大，所以\(S_{db}\)也会较大，而相比之下，\(dW\)会小一些，亦或\(dW\)平方会小一些，因此\(S_{dW}\)会小一些，结果就是纵轴上的更新要被一个较大的数相除，就能消除摆动，而水平方向的更新则被较小的数相除。

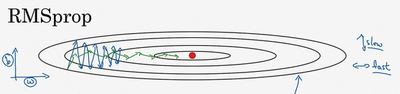
RMSprop的影响就是的更新最后会变成这样（绿色线），纵轴方向上摆动较小，而横轴方向继续推进。还有个影响就是，可以用一个更大学习率\(a\)，然后加快学习，而无须在纵轴上垂直方向偏离。

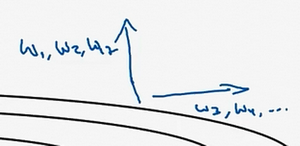
要说明一点，一直把纵轴和横轴方向分别称为\(b\)和\(W\)，只是为了方便展示而已。实际中，会处于参数的高维度空间，所以需要消除摆动的垂直维度，需要消除摆动，实际上是参数\(W_1\)，\(W_2\)等的合集，水平维度可能\(W_3\)，\(W_4\)等等，因此把\(W\)和\(b\)分开只是方便说明。实际中\(dW\)是一个高维度的参数向量，\(db\)也是一个高维度参数向量，但是的直觉是，在要消除摆动的维度中，最终要计算一个更大的和值，这个平方和微分的加权平均值，所以最后去掉了那些有摆动的方向。所以这就是RMSprop，全称是均方根，因为将微分进行平方，然后最后使用平方根。

最后再就这个算法说一些细节的东西，然后再继续。接下来，会将RMSprop和Momentum结合起来，在Momentum中采用超参数\(\beta\)，为了避免混淆，现在不用\(\beta\)，而采用超参数\(\beta_{2}\)以保证在Momentum和RMSprop中采用同一超参数。要确保的算法不会除以0，如果\(S_{dW}\)的平方根趋近于0怎么办？得到的答案就非常大，为了确保数值稳定，在实际操练的时候，要在分母上加上一个很小很小的\(\varepsilon\)，\(\varepsilon\)是多少没关系，\(10^{-8}\)是个不错的选择，这只是保证数值能稳定一些，无论什么原因，都不会除以一个很小很小的数。所以RMSprop跟Momentum有很相似的一点，可以消除梯度下降中的摆动，包括mini-batch梯度下降，并允许使用一个更大的学习率\(a\)，从而加快的算法学习速度。

所以学会了如何运用RMSprop，这是给学习算法加速的另一方法。关于RMSprop的一个有趣的事是，它首次提出并不是在学术研究论文中，而是在多年前Jeff Hinton在Coursera的课程上。想Coursera并不是故意打算成为一个传播新兴的学术研究的平台，但是却达到了意想不到的效果。就是从Coursera课程开始，RMSprop开始被人们广为熟知，并且发展迅猛。

讲过了Momentum，讲了RMSprop，如果二者结合起来，会得到一个更好的优化算法