TensorFlow线性回归
目录
数据可视化
梯度下降
结果可视化
|
数据可视化 |
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围
num_points = 1000
vectors_set = []
for i in range(num_points):
x1 = np.random.normal(0.0, 0.55)
y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03)
vectors_set.append([x1, y1]) # 生成一些样本
x_data = [v[0] for v in vectors_set]
y_data = [v[1] for v in vectors_set] plt.scatter(x_data,y_data,c='r')
plt.show()
|
梯度下降 |
# -*- coding: utf-8 -*-
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围
num_points = 1000
vectors_set = []
for i in range(num_points):
x1 = np.random.normal(0.0, 0.55)
y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03)
vectors_set.append([x1, y1]) # 生成一些样本
x_data = [v[0] for v in vectors_set]
y_data = [v[1] for v in vectors_set] # 生成1维的W矩阵,取值是[-1,1]之间的随机数
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name='W')
# 生成1维的b矩阵,初始值是0
b = tf.Variable(tf.zeros([1]), name='b')
# 经过计算得出预估值y
y = W * x_data + b # 以预估值y和实际值y_data之间的均方误差作为损失
loss = tf.reduce_mean(tf.square(y - y_data), name='loss')
# 采用梯度下降法来优化参数
optimizer = tf.train.GradientDescentOptimizer(0.5) #参数是学习率
# 训练的过程就是最小化这个误差值
train = optimizer.minimize(loss, name='train') sess = tf.Session() init = tf.global_variables_initializer()
sess.run(init) # 初始化的W和b是多少
print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss))
# 执行20次训练
for step in range(20):
sess.run(train)
# 输出训练好的W和b
print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss))
'''
W = [ 0.72134733] b = [ 0.] loss = 0.204532
W = [ 0.54246926] b = [ 0.31014919] loss = 0.0552976
W = [ 0.41924465] b = [ 0.30693138] loss = 0.029155
W = [ 0.33045709] b = [ 0.30471471] loss = 0.0155833
W = [ 0.26648441] b = [ 0.30311754] loss = 0.00853772
W = [ 0.22039121] b = [ 0.30196676] loss = 0.00488007
W = [ 0.18718043] b = [ 0.3011376] loss = 0.00298124
W = [ 0.16325161] b = [ 0.30054021] loss = 0.00199547
W = [ 0.14601055] b = [ 0.30010974] loss = 0.00148373
W = [ 0.13358814] b = [ 0.29979959] loss = 0.00121806
W = [ 0.12463761] b = [ 0.29957613] loss = 0.00108014
W = [ 0.11818863] b = [ 0.29941514] loss = 0.00100854
W = [ 0.11354206] b = [ 0.29929912] loss = 0.000971367
W = [ 0.11019413] b = [ 0.29921553] loss = 0.00095207
W = [ 0.10778191] b = [ 0.29915532] loss = 0.000942053
W = [ 0.10604387] b = [ 0.29911193] loss = 0.000936852
W = [ 0.10479159] b = [ 0.29908064] loss = 0.000934153
W = [ 0.1038893] b = [ 0.29905814] loss = 0.000932751
W = [ 0.10323919] b = [ 0.2990419] loss = 0.000932023
W = [ 0.10277078] b = [ 0.29903021] loss = 0.000931646
W = [ 0.10243329] b = [ 0.29902178] loss = 0.00093145
'''
|
结果可视化 |
# -*- coding: utf-8 -*-
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt # 随机生成1000个点,围绕在y=0.1x+0.3的直线周围
num_points = 1000
vectors_set = []
for i in range(num_points):
x1 = np.random.normal(0.0, 0.55)
y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03)
vectors_set.append([x1, y1]) # 生成一些样本
x_data = [v[0] for v in vectors_set]
y_data = [v[1] for v in vectors_set] # 生成1维的W矩阵,取值是[-1,1]之间的随机数
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name='W')
# 生成1维的b矩阵,初始值是0
b = tf.Variable(tf.zeros([1]), name='b')
# 经过计算得出预估值y
y = W * x_data + b # 以预估值y和实际值y_data之间的均方误差作为损失
loss = tf.reduce_mean(tf.square(y - y_data), name='loss')
# 采用梯度下降法来优化参数
optimizer = tf.train.GradientDescentOptimizer(0.5) #参数是学习率
# 训练的过程就是最小化这个误差值
train = optimizer.minimize(loss, name='train') sess = tf.Session() init = tf.global_variables_initializer()
sess.run(init) # 初始化的W和b是多少
print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss))
# 执行20次训练
for step in range(20):
sess.run(train)
# 输出训练好的W和b
print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss)) plt.scatter(x_data,y_data,c='r')
plt.plot(x_data,sess.run(W)*x_data+sess.run(b))
plt.show()
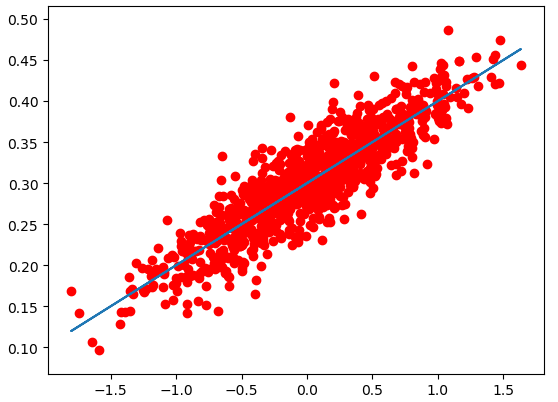
TensorFlow线性回归的更多相关文章
- [tensorflow] 线性回归模型实现
在这一篇博客中大概讲一下用tensorflow如何实现一个简单的线性回归模型,其中就可能涉及到一些tensorflow的基本概念和操作,然后因为我只是入门了点tensorflow,所以我只能对部分代码 ...
- python,tensorflow线性回归Django网页显示Gif动态图
1.工程组成 2.urls.py """Django_machine_learning_linear_regression URL Configuration The ` ...
- tensorflow 线性回归解决 iris 2分类
# Combining Everything Together #---------------------------------- # This file will perform binary ...
- 1.tensorflow——线性回归
tensorflow 1.一切都要tf. 2.只有sess.run才能生效 import tensorflow as tf import numpy as np import matplotlib.p ...
- tensorflow 线性回归 iris
线性拟合
- TensorFlow简要教程及线性回归算法示例
TensorFlow是谷歌推出的深度学习平台,目前在各大深度学习平台中使用的最广泛. 一.安装命令 pip3 install -U tensorflow --default-timeout=1800 ...
- TensorFlow API 汉化
TensorFlow API 汉化 模块:tf 定义于tensorflow/__init__.py. 将所有公共TensorFlow接口引入此模块. 模块 app module:通用入口点脚本. ...
- tfboys——tensorflow模块学习(三)
tf.estimator模块 定义在:tensorflow/python/estimator/estimator_lib.py 估算器(Estimator): 用于处理模型的高级工具. 主要模块 ex ...
- TensorFlow — 相关 API
TensorFlow — 相关 API TensorFlow 相关函数理解 任务时间:时间未知 tf.truncated_normal truncated_normal( shape, mean=0. ...
随机推荐
- Django框架——进阶之AJAX
<script>$("#b1").on("click", function () { // 点击 id是b1的按钮要做的事儿 var i1 = $( ...
- upupw : Apache Php5.5 的使用
1. 官网下载 1. 官网下载 apache php5.5点击下载 但是 现在有时候打不开,所以提供以下方法 2. 百度云网盘下载 https://pan.baidu.com/s/1eQ2k1Su ...
- orcle_day02
第三章:单值函数 函数分为: 1.单值函数 1.字符函数 2.日期函数 3.转换函数 4.数字函数 2.分组函数(后面的章节再做学习) 哑表dual dual是一个虚拟表,用来构成select的语法规 ...
- 使用Ant打包工具
由于使用java,javac,jar等工具进行编译打包,即繁琐低效又容易出错,因此Ant出现了.Ant的出现就是专门为了打包编译java代码的,使用之前得稍微学一下.Ant的运行起来主要是依靠配置文件 ...
- SpringBoot布道系列 | 目录汇总 | 2019持续更新ing
SpringBoot 基础教程 | 三大推荐理由 1.文章内容均为原创,结合官方文档和实战经验编写. 2.文章结构经过细致整理,对新人学习更加友好. 3.精选常用技术,不求全面,但求精华!! Spri ...
- Hibrenate实现根据实体类自动创建表或添加字段
Hibernate支持自动建表,在开发阶段很方便,可以保证hbm与数据库表结构的自动同步. 实现: 在配置hibernate的配置文件中将hbm2ddl.auto设置为update,如:Xml代码&l ...
- date( ) 日期函数
date('Y-m-dT2:00') 实际时间为14:00 date('Y-m-d 2:00') 实际时间为2:00 扩展:每天的时间戳秒数为 86400
- 利用docker 部署项目
docker_tomcat_jdk 7.0 1.6 app admin && api 1.yum install docker 2.service docker start 3.创建文 ...
- python--Excel模块xlwings
安装:pip install xlwings 基本操作: xlwings的特色: xlwings能够非常方便的读写Excel文件中的数据,并且能够进行单元格格式的修改 可以和matplotlib以及p ...
- std::setw(size)与std::setfill(char)
头文件:#include <iostream>#include <iomanip>using namespace std; 功能: std::setw :需要填充多少个字符, ...
