简单QR分解之Gram-Schmit正交化&&Householder变换&&Givens Rotation变换&&计算步骤


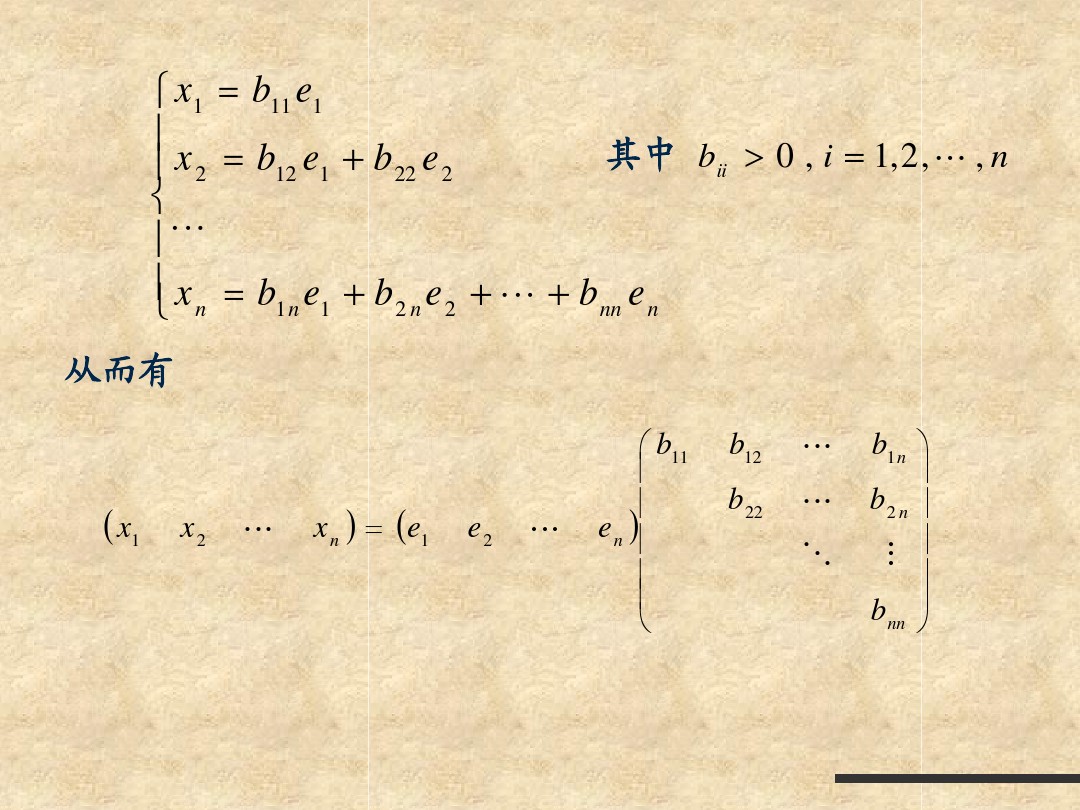




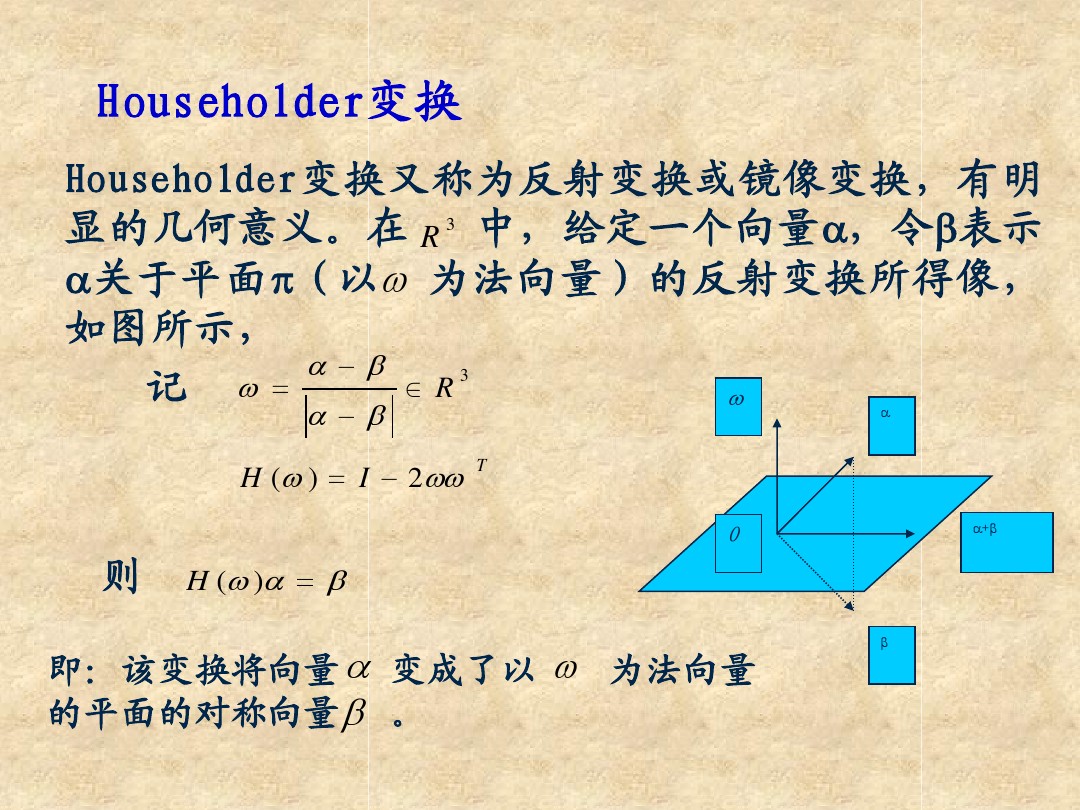





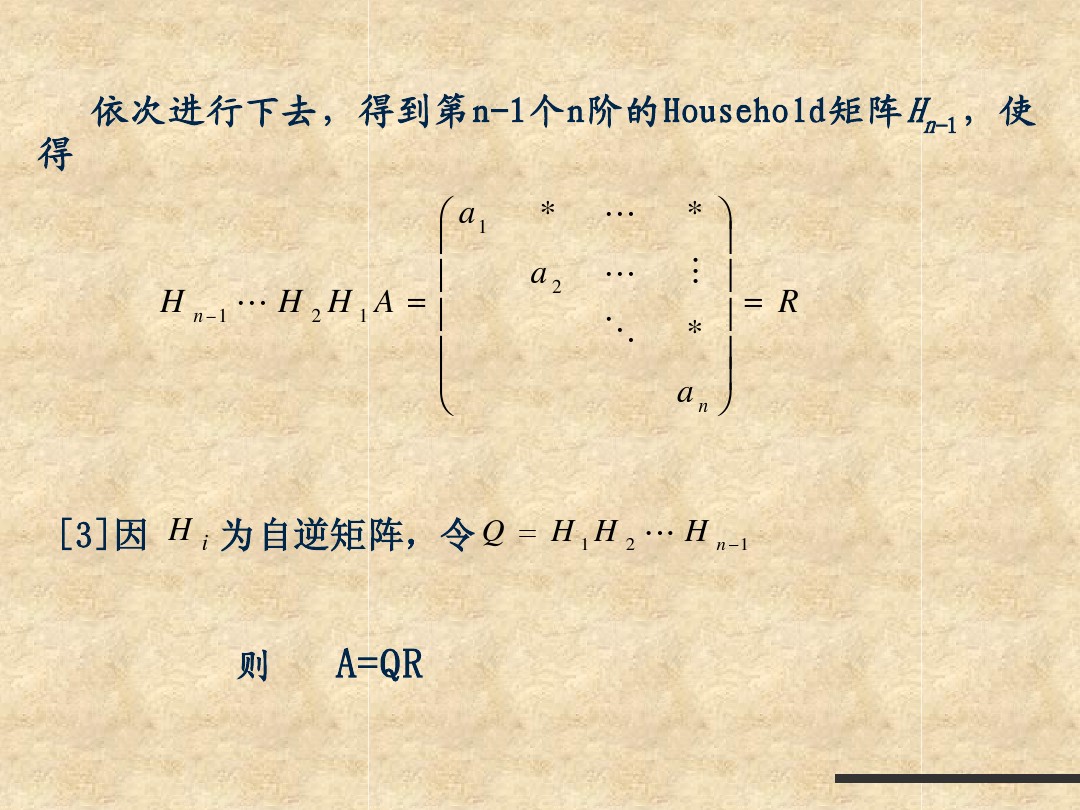



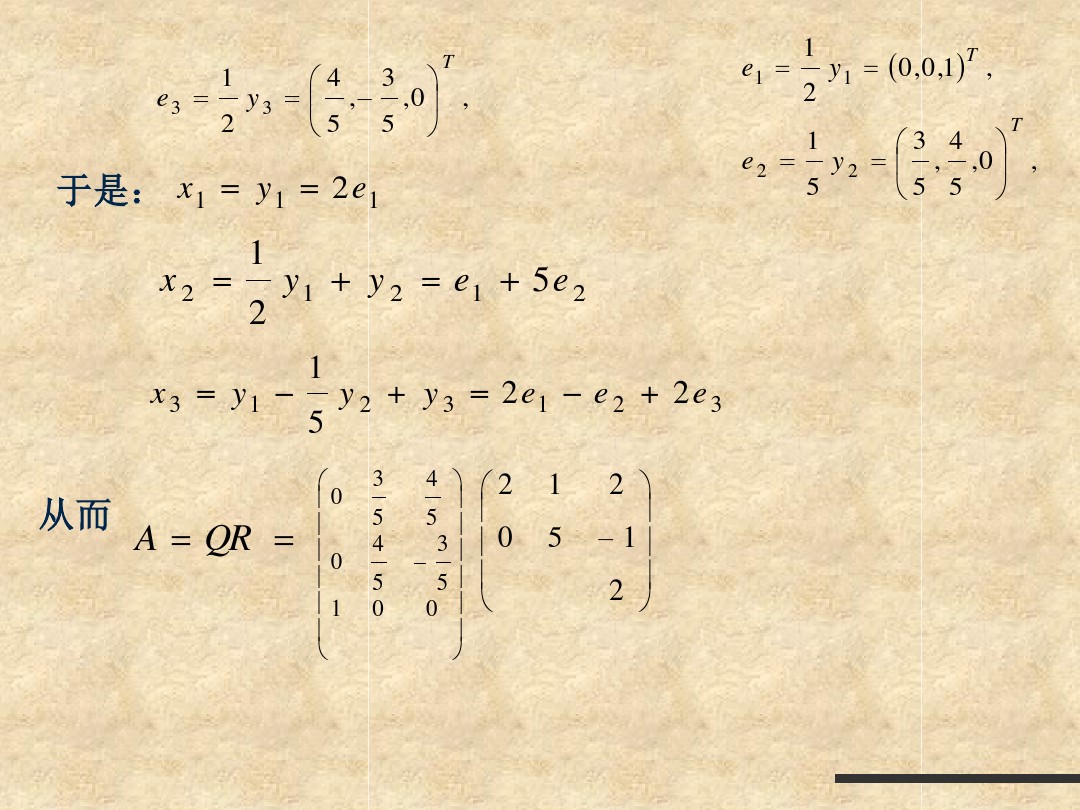

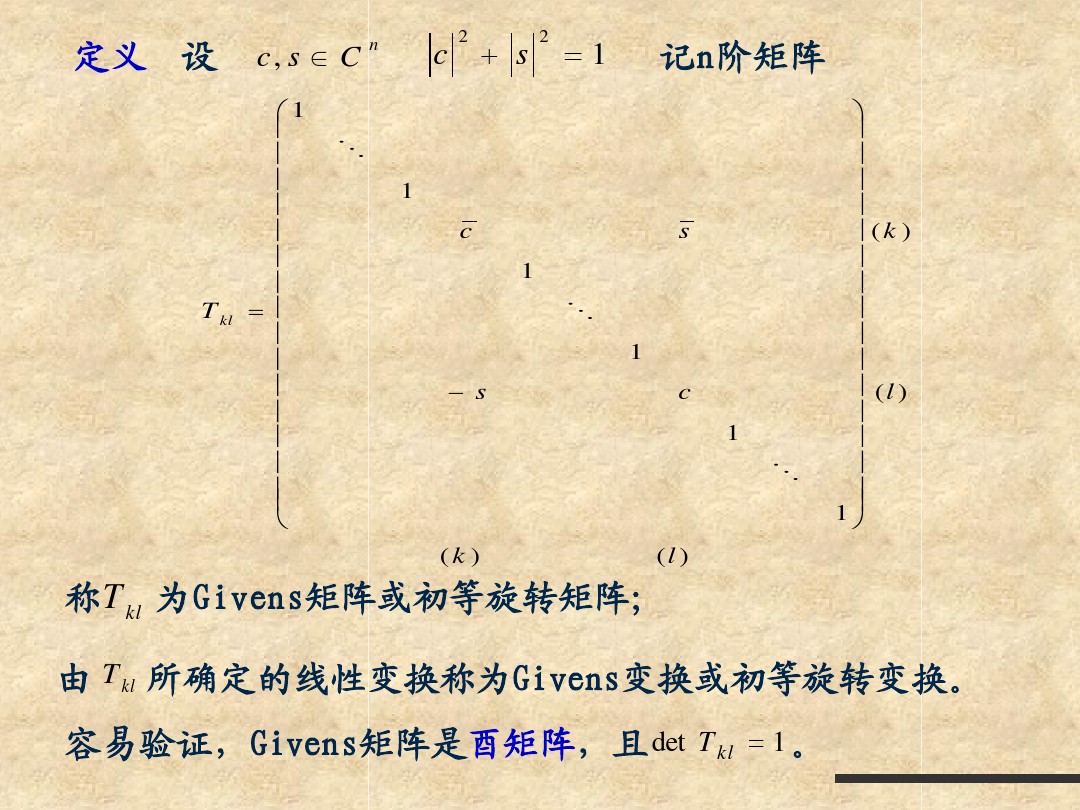





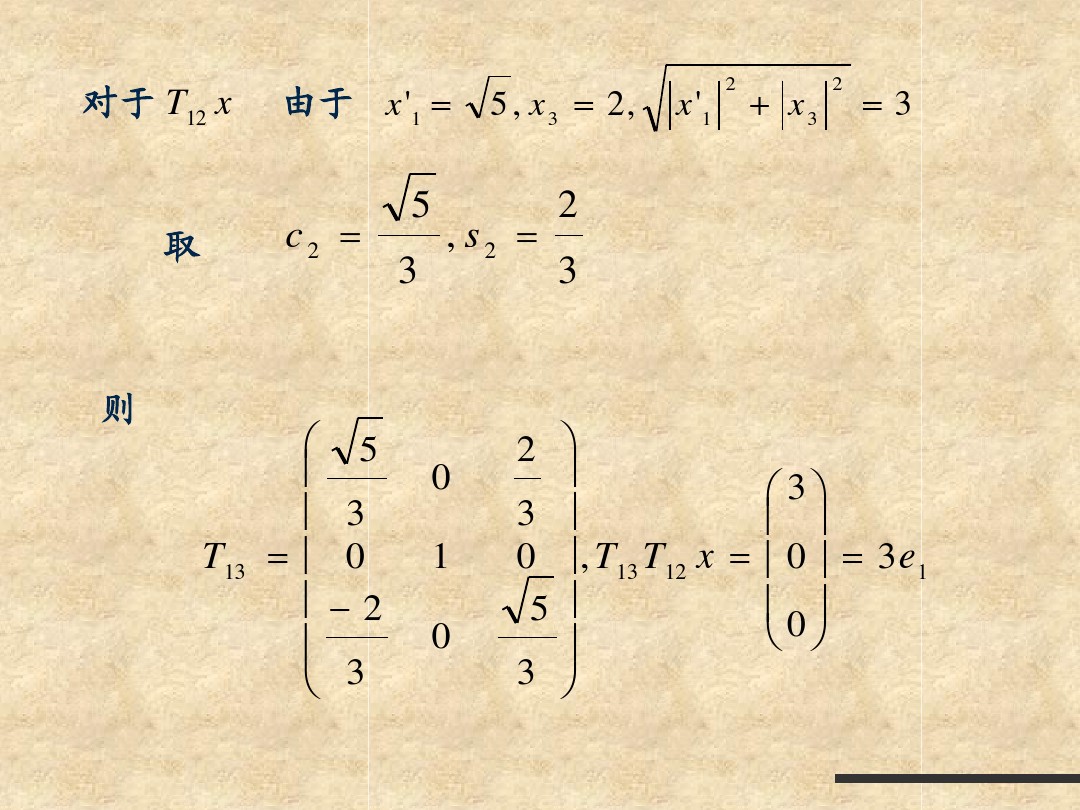

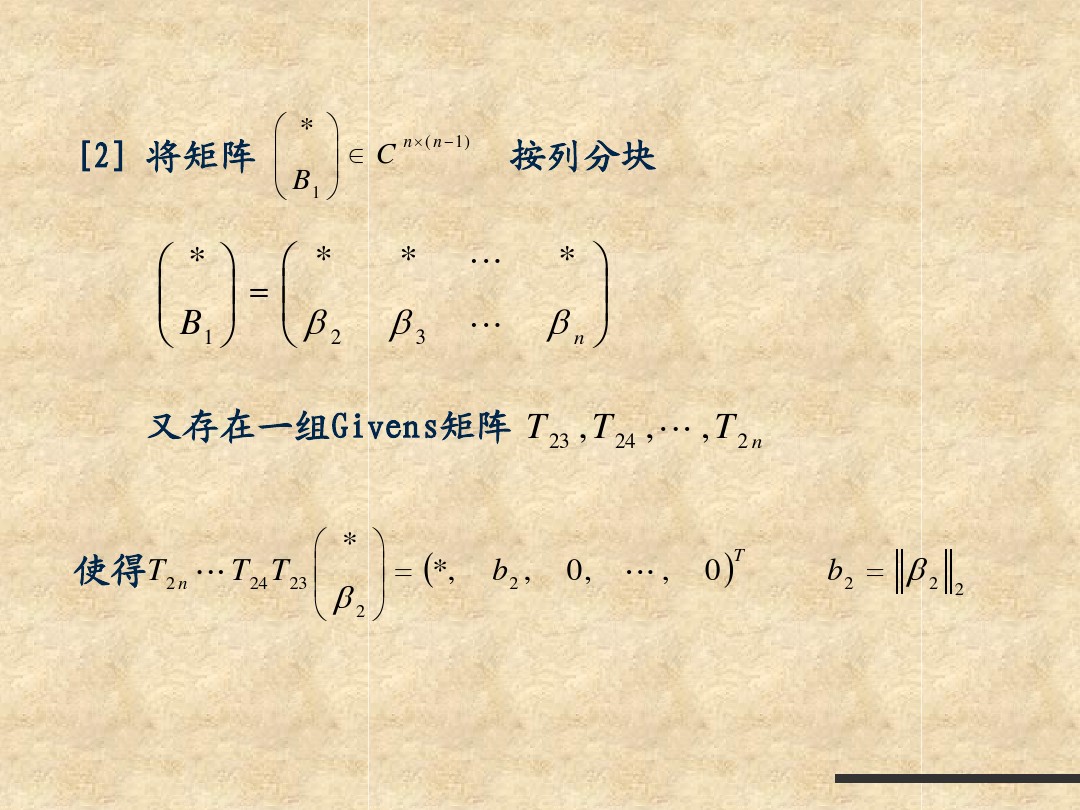


简单QR分解之Gram-Schmit正交化&&Householder变换&&Givens Rotation变换&&计算步骤的更多相关文章
- 机器学习中的矩阵方法03:QR 分解
1. QR 分解的形式 QR 分解是把矩阵分解成一个正交矩阵与一个上三角矩阵的积.QR 分解经常用来解线性最小二乘法问题.QR 分解也是特定特征值算法即QR算法的基础.用图可以将分解形象地表示成: 其 ...
- QR分解与最小二乘
主要内容: 1.QR分解定义 2.QR分解求法 3.QR分解与最小二乘 4.Matlab实现 一.QR分解 R分解法是三种将矩阵分解的方式之一.这种方式,把矩阵分解成一个正交矩阵与一个上三角矩阵的 ...
- QR分解与最小二乘(转载自AndyJee)
转载网址:http://www.cnblogs.com/AndyJee/p/3846455.html 主要内容: 1.QR分解定义 2.QR分解求法 3.QR分解与最小二乘 4.Matlab实现 一. ...
- QR分解
从矩阵分解的角度来看,LU和Cholesky分解目标在于将矩阵转化为三角矩阵的乘积,所以在LAPACK种对应的名称是trf(Triangular Factorization).QR分解的目的在 ...
- QR 分解
将学习到什么 介绍了平面旋转矩阵,Householder 矩阵和 QR 分解以入相关性质. 预备知识 平面旋转与 Householder 矩阵是特殊的酉矩阵,它们在建立某些基本的矩阵分解过程中起着 ...
- QR分解迭代求特征值——原生python实现(不使用numpy)
QR分解: 有很多方法可以进行QR迭代,本文使用的是Schmidt正交化方法 具体证明请参考链接 https://wenku.baidu.com/view/c2e34678168884868762d6 ...
- 矩阵QR分解
1 orthonormal 向量与 Orthogonal 矩阵 orthonormal 向量定义为 ,任意向量 相互垂直,且模长为1: 如果将 orthonormal 向量按列组织成矩阵,矩阵为 ...
- 矩阵的QR分解(三种方法)Python实现
1.Gram-Schmidt正交化 假设原来的矩阵为[a,b],a,b为线性无关的二维向量,下面我们通过Gram-Schmidt正交化使得矩阵A为标准正交矩阵: 假设正交化后的矩阵为Q=[A,B],我 ...
- 【矩阵】RQ/QR 分解
Multiple View Geometry in Computer Vision A.4.1.1 (page 579) 将一个 3x3 矩阵 $ A $ 进行 RQ 分解是将其分解成为一个上三角阵 ...
随机推荐
- 大杀器:VS2017 查看或调试liunx代码(转载)
From:https://blog.csdn.net/mumufan05/article/details/80094637 上一篇简单介绍了vs2017新建一个linux的工程,本编将介绍一下如何管理 ...
- logstash配置
input { #You must define a [type], otherwise you cannot get a field to cut. tcp { port => 5045 ty ...
- python之bytes和string
转自:https://www.cnblogs.com/skiler/p/6687337.html 1.bytes主要是给在计算机看的,string主要是给人看的 2.中间有个桥梁就是编码规则,现在大趋 ...
- Xmanager power suit 6 最新版注册激活
Xmanager Power Suit 6.0.0012 最新版注册激活,长期更新 操作步骤 Xmanger Power Suit 官方 其实有两种 .exe 文件,一个是用于试用的,在注册的时候不能 ...
- JavaSe: 不要小看了 Serializable
Java中,一个类要支持序列化,我们通常实现Serializable.在使用Serializable,应当制定一个SerialVersionUID,用于代表类的版本.如果不指定会有什么影响呢?在了解这 ...
- IOC注解开发与XML整合
区别: xml:可以适用于任何场景,结构清晰,方便维护 注解:开发方便,快速.有些地方适用不了,这个类不是自己提供的(比如源码提供的类) xml和注解整合开发,各取所长 xml使用于对bean进行管理 ...
- WPF设计の画刷(Brush)
一.什么是画刷 画刷是是一种渲染方式,用于填充图形形状,如矩形.椭圆.扇形.多边形和封闭路径.在GDI+中,画刷分为以下几种:SolidBrush,TextureBrush,HatchBrush,Li ...
- 绝版珍珍藏:web前端技术学习指南
绝版珍珍藏:web前端技术学习指南 优秀的Web前端开发工程师要在知识体系上既要有广度和深度!应该具备快速学习能力. 前端开发工程师不仅要掌握基本的Web前端开发技术,网站性能优化.SEO和服务器端的 ...
- 定时器 setTimeout()超时调用和 setInterval()间歇调用
JavaScript是单线程语言,但它允许通过设置定时器,也就是设置超时值和间歇时间来调度代码在特定的时刻执行.前者是在指定的时间过后执行代码,而后者则是每隔指定的时间就执行一次代码. 超时调用需要使 ...
- 《JAVA程序设计》_第一周学习总结
20175217吴一凡 <java程序设计> 第一周学习总结 虽然已经做好了心理准备,但第一周的学习任务着实让我忙了整整三天,还是挺充实的吧.寒假已经在自己的电脑上安装好了虚拟机,我就在我 ...
