ML 徒手系列 最大似然估计

1、最大似然估计数学定义：

　　假设总体分布为f(x,θ),X1,X2...Xn为总体采样得到的样本。其中X1,X2...Xn独立同分布，可求得样本的联合概率密度函数为：

　　

　　其中θ是需要求得的未知量，x_i是样本值。

　　此时，L(x,θ)是关于θ的函数，称之为似然函数。

　　求参数θ值使得似然函数值取最大值，这种方法称之为最大似然估计。》》MLE

2、如何求解最大似然估计

　　其中x是已知的，θ是需要求的变量值。如果最大似然函数可导，可以通过对θ求导的方式，取得L(x,θ)的极值。

　　在实际中为了方便计算，往往先对L(x,θ)取对数：

　　　　加入求导：

3、使用MLE推导逻辑回归

　　逻辑回归中使用sigmoid函数，将输出值确定在范围0到1之间。此时输出的值相当于概率中某一个样本的值。即上述所讲的X1,X2...Xn。

而sigmoid函数中所需要求的w，即为似然函数中的θ。

　　有如下公式：

　　　　1、sigmoid函数

　　　　　　此时没有截距b，加入后在归一化时会被约掉，所以干脆不使用b。

　　　　2、sigmoid求导

　　　　　　　　　3、对数似然函数　　　　

　　　　　　概率分布为：

　　　　　　将上面两式子写作联合：

　　　　　　联合概率密度函数为：

　　　　　　

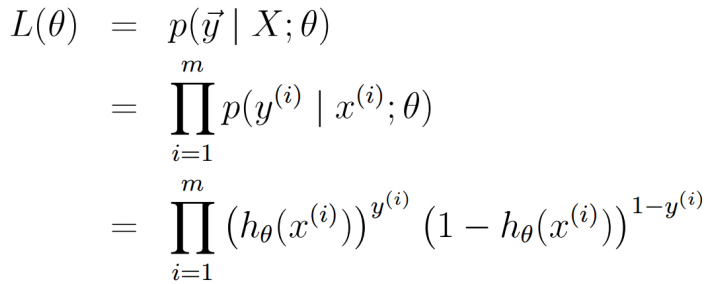
　　　　　　构建似然函数：

　　4、求解MLE

　　5、与UFLDL中的RL结合，改变某些表述：

　　　　概率分布：　　　　

　　　　似然函数：

　　　　

　　　　求解MLE:

　　　　矩阵形式：

得到似然函数对θ的导数后，使用梯度下降法来更新θ，使得最终的结果接近于label。

4、使用似然估计推导softma

　　（此处使用UFLDL中的公式，敲公式好麻烦。。。）

　　（1）概率

　　（2）似然函数

　　（3）对似然函数关于θq求导

　　　　　　似然函数展开：

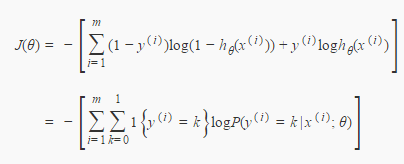
　　　　　　求导：

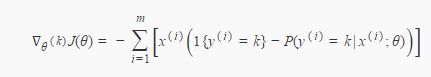
最后，同样使用梯度下降法来求最优θ。

LR可以使用最大熵来推导，在后续给出。

参考：

UFLDL

有机会，会做一个UFLDL的总结博客。