雅礼集训 Day1 T3 画作 解题报告

画作

题目描述

小\(\mathrm{G}\)的喜欢作画,尤其喜欢仅使用黑白两色作画.

画作可以抽象成一个\(r\times c\)大小的\(01\)矩阵.现在小\(\mathrm{G}\)构思好了他的画作,准备动笔开始作画.初始时画布是全白的,他每一次下笔可以将一个四联通的部分涂成黑色或白色.

你需要告诉他,在给出的构思下,他最少需要下笔多少次才能完成画作.

注:四联通部分表示这个部分的任意两个点都可以通过四联通的方式到达.

输入输出格式

输入格式

第一行两个正整数\(r,c\).

接下来\(r\)行,每行\(c\)个字符, 表示目标画作.

输出格式

输出一行一个正整数,表示最少需要的下笔步数.

说明：

• \(\mathrm{Subtask 1 (19pts)}:r\times c\le 15\).
• \(\mathrm{Subtask 2 (7pts)}:r=1\).
• \(\mathrm{Subtask 3 (25pts)}:r,c\le 30\).
• \(\mathrm{Subtask 4 (49pts)}: r,c\le 50\).

---

各方面我都不知道说什么的题目。

首先需要猜出一个结论：

一定存在一种最优策略，使得每次操作的区域是上一次操作区域的子集且操作颜色相反。

题解的证明不是很懂。

大概就是证明这两种简单的情况

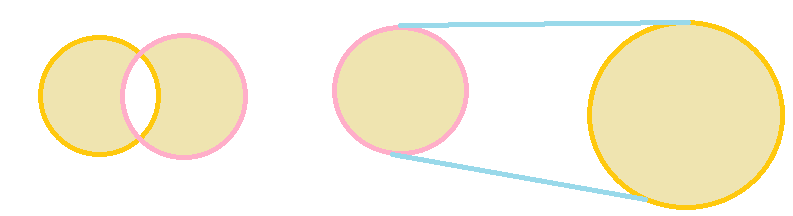
然后推到一些复杂一点的情况进行归纳

还是把题解的证明放一放吧。

然后枚举每个点作为最后一次被染色的点的情况。

把四联通的相同颜色边权置0，不同颜色置1

跑最短路，然后取最远的点作为答案，对每个点的答案取最小值即可

注意这里最短路要跑01BFS

复杂度:\(O(n^4)\)

---

Code:

#include <cstdio>
#include <cstring>
const int N=52;
const int inf=0x3f3f3f3f;
const int dx[5]={0,-1,0,1,0};
const int dy[5]={0,0,1,0,-1};
int n,m,g[N][N];
int to[N*N][5][2],ans=inf;
int min(int x,int y){return x<y?x:y;}
int max(int x,int y){return x>y?x:y;}
int cal(int i,int j)
{
    return m*(i-1)+j;
}
int q[N*N*2],l,r,dis[N*N];
int bfs(int s)
{
    int mx=0;
    l=50*50,r=l-1;
    q[++r]=s;
    memset(dis,inf,sizeof(dis));
    dis[s]=0;
    while(l<=r)
    {
        int now=q[l++];
        for(int i=1;i<=4;i++)
        {
            int w=to[now][i][0],v=to[now][i][1];
            if(dis[v]!=inf) continue;
            if(w==0)
                dis[v]=dis[now],q[--l]=v;
            else if(w==1)
                dis[v]=dis[now]+1,q[++r]=v;
        }
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(g[i][j])
                mx=max(mx,dis[cal(i,j)]);
    return mx+1;
}
int main()
{
    scanf("%d%d",&n,&m);
    char c;
    for(int i=1;i<=n;i++)
    {
        scanf("\n");
        for(int j=1;j<=m;j++)
        {
            scanf("%c",&c);
            g[i][j]=c-'0';
        }
    }
    memset(to,-1,sizeof(to));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            for(int k=1;k<=4;k++)
            {
                int ti=i+dx[k],tj=j+dy[k];
                if(ti<=0||ti>n||tj<=0||tj>m) continue;
                int u=cal(i,j),v=cal(ti,tj);
                to[u][k][0]=g[i][j]!=g[ti][tj];
                to[u][k][1]=v;
            }
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            ans=min(ans,bfs(cal(i,j)));
    printf("%d\n",ans);
    return 0;
}

---

2018.10.9