CF24D Broken robot

题目链接

题意

有一个\(n \times m\)的矩阵。机器人从点\((x,y)\)开始等概率的往下,往右,往左走或者不动。如果再第一列，那么不会往左走，再第m列不会往右走。也就是说机器人不会走出这个格子。走到最后一行会停止。求出机器人期望行走的步数。

思路

设\(f[i][j]\)表示从\((i,j)\)走到最后一行的期望步数。

显然最后一行的答案为0

然后考虑其他行。假设\(j!=m\)并且\(j!=1\)那么有

\[f[i][j]=1+\frac{1}{4}(f[i][j+1]+f[i][j-1]+f[i][j]+f[i+1][j])
\]

然后这个\(dp\)具有后效性，无法直接转移

通分移项可得

\[f[i + 1][j] + 4 = 3f[i][j] - f[i][j - 1] - f[i][j + 1]
\]

这样对于每一行我们就可以列出来一个\(m\)元的方程组。

然后发现\(f\)数组的每一行都可以用一次高斯消元解出来。

\(j=1\)或者\(j=m\)？？

和上面一样的思路，稍微改一下\(dp\)方程即可

如下

\[f[1][j] + 3=2f[1][j] - f[1][j+1]
\]

\[f[m][j] + 3=2f[m][j] - f[m][j-1]
\]

复杂度？？？

因为这个高斯消元的矩阵列出来是一个这样的矩阵

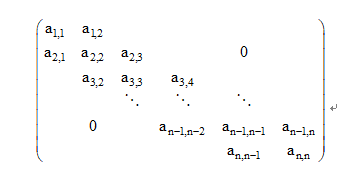
所以其实是可以\(O(m)\)的解的。

所以总复杂度是\(O(nm)\)

代码

这是一份取模版(模数为\(998244353\))的代码,直接交到\(CF\)上会\(WA\)！！！

/*
* @Author: wxyww
* @Date:   2019-03-16 08:00:47
* @Last Modified time: 2019-03-16 16:20:43
*/
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>
#include<ctime>
using namespace std;
typedef long long ll;
const int mod = 998244353,N = 1010;
#define int ll
ll read() {
	ll x=0,f=1;char c=getchar();
	while(c<'0'||c>'9') {
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9') {
		x=x*10+c-'0';
		c=getchar();
	}
	return x*f;
}
int Bx,By,n,m,f[N][N],g[N][N];
ll qm(ll x,ll y) {
	ll ans = 1;
	for(;y;y >>= 1,x = x * x % mod)
		if(y & 1) ans = ans * x % mod;
	return ans;
}
void solve(int x) {

	g[1][m + 1] = f[x + 1][1] + 3;
	g[m][m + 1] = f[x + 1][m] + 3;
	for(int i = 2;i < m;++i) g[i][m + 1] = f[x + 1][i] + 4;

	f[x][1] = g[1][1];f[x][2] = g[1][2];f[x][m + 1] = g[1][m + 1];
	for(int i = 2;i <= m;++i) {
		int k1 = f[x][i - 1],k2 = g[i][i - 1];
		f[x][i - 1] = (1ll * f[x][i - 1] * k2 % mod - (1ll * g[i][i - 1] * k1 % mod) + mod) % mod;
		f[x][i] = (1ll * f[x][i] * k2 % mod - (1ll * g[i][i] * k1 % mod) + mod)% mod;
		if(i != m)
		f[x][i + 1] = (1ll * f[x][i + 1] * k2 % mod - (1ll * g[i][i + 1] * k1 % mod) + mod) % mod;
		f[x][m + 1] = (1ll * f[x][m + 1] * k2 % mod - (1ll * g[i][m + 1] * k1 % mod) + mod) % mod;

	}

	f[x][m] = 1ll * f[x][m + 1] * qm(f[x][m],mod - 2) % mod;

	f[x][m - 1] = 1ll * (g[m][m + 1] - (1ll * g[m][m] * f[x][m] % mod) + mod) % mod * qm(g[m][m - 1],mod - 2) % mod;

	for(int i = m - 1;i > 1;--i)
		f[x][i - 1] = ((g[i][m + 1] - ((f[x][i] * g[i][i] % mod + mod)% mod) - (f[x][i + 1] * g[i][i + 1] % mod)) % mod + mod) % mod * qm(g[i][i - 1],mod - 2) % mod;
}
signed main() {
	n = read(),m = read();
	Bx = read(),By = read();

	if(m == 1) {printf("%lld\n",2ll * (n - Bx) % mod);	return 0;}

	g[1][1] = 2;g[1][2] = mod - 1;
	g[m][m - 1] = mod - 1,g[m][m] = 2;
	for(int i = 2;i < m;++i)
		g[i][i] = 3,g[i][i + 1] = mod - 1,g[i][i - 1] = mod - 1;

	for(int i = n - 1;i >= Bx;--i) solve(i);

	cout<<f[Bx][By];
	return 0;
}