2018.09.06 警卫安排（树形dp）

描述

太平王世子事件后，陆小凤成了皇上特聘的御前一品侍卫。 皇宫以午门为起点，直到后宫嫔妃们的寝宫，呈一棵树的形状；有边直接相连的宫殿可以互相望见。大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。 可是陆小凤手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。



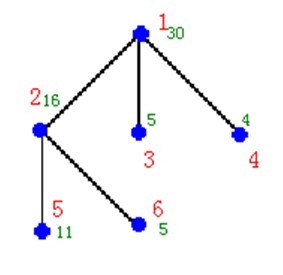
编程任务：帮助陆小凤布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

输入

输入文件中数据表示一棵树，描述如下：

第1行 n，表示树中结点的数目。

第2行至第n+1行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号i（0< I<=N），在该宫殿安置侍卫所需的经费K，该点的儿子数M，接下来M个数，分别是这个节点的M个儿子的标号R1，R2，…，RM。对于一个n（0 < n<=1500）个结点的树，结点标号在1到n之间，且标号不重复。

输出

输出文件仅包含一个数，为所求的最少的经费。

样例输入

6

1 30 3 2 3 4

2 16 2 5 6

3 5 0

4 4 0

5 11 0

6 5 0

样例输出

25

---

树形dp经典题。

注意要考虑儿子和父亲的影响。

用f[i][0]表示选择当前节点的最优值

f[i][1]表示当前节点父亲被选，自己不被选的最优值。

f[i][2]表示当前节点与当前节点父亲均不被选的最优值。

注意第三个至少有一个儿子会被选。

于是有：

f[i][0]=w[i]+∑vmin(f[v][0],f[v][1],f[v][2])" role="presentation" style="position: relative;">f[i][0]=w[i]+∑min(f[v][0],f[v][1],f[v][2])vf[i][0]=w[i]+∑vmin(f[v][0],f[v][1],f[v][2])

f[i][1]=w[i]+∑vmin(f[v][0],f[v][2])" role="presentation" style="position: relative;">f[i][1]=w[i]+∑min(f[v][0],f[v][2])vf[i][1]=w[i]+∑vmin(f[v][0],f[v][2])

f[i][2]=w[i]+∑vmin(f[v][0],f[v][2])" role="presentation" style="position: relative;">f[i][2]=w[i]+∑min(f[v][0],f[v][2])vf[i][2]=w[i]+∑vmin(f[v][0],f[v][2])且至少有一个儿子被选。

代码：

#include<bits/stdc++.h>
#define N 2005
using namespace std;
inline int read(){
    int ans=0;
    char ch=getchar();
    while(!isdigit(ch))ch=getchar();
    while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
    return ans;
}
int n,first[N],f[N][3],cnt=0,w[N],rt;
bool vis[N];
struct edge{int v,next;}e[N];
inline void add(int u,int v){e[++cnt].v=v,e[cnt].next=first[u],first[u]=cnt;}
inline int min(int a,int b){return a<b?a:b;}
inline int dfs(int p,int k){
    if(~f[p][k])return f[p][k];
    f[p][k]=(k==0)?w[p]:(k==1?0:2e9);
    for(int i=first[p];i;i=e[i].next){
        int v=e[i].v;
        if(!k)f[p][k]+=min(dfs(v,0),min(dfs(v,1),dfs(v,2)));
        else if(k==1)f[p][k]+=min(dfs(v,0),dfs(v,2));
        else f[p][k]=min(f[p][k],dfs(p,1)-min(dfs(v,0),dfs(v,2))+f[v][0]);
    }
    return f[p][k];
}
int main(){
    n=read(),memset(f,-1,sizeof(f));
    for(int i=1;i<=n;++i){
        int u=read(),v,k;
        w[u]=read(),k=read();
        for(int j=1;j<=k;++j)v=read(),add(u,v),vis[v]=true;
    }
    for(int i=1;i<=n;++i)if(!vis[i]){rt=i;break;}
    cout<<min(dfs(rt,0),dfs(rt,2));
    return 0;
}