机器学习数学知识中令人费解的notation符号注解
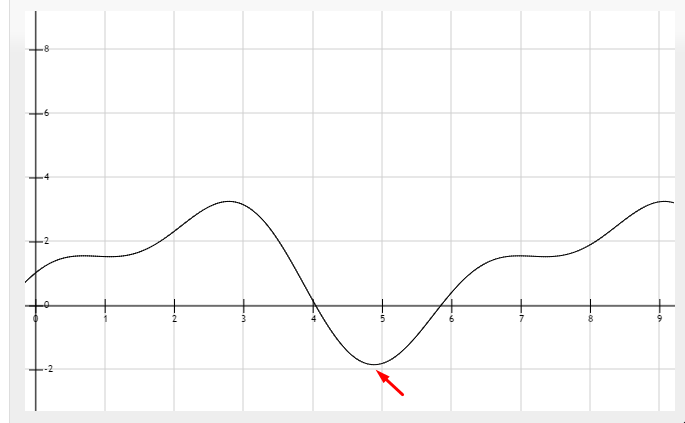
$argmin_xf(x), min(f(x))$
$min(f(x))$的意思是函数$f(x)$的最小值
$argmin$的意思是返回使得表达式取得最小值时对应的输入变量值。例如$argmin_xf(x)$等于当$f(x)$取得最小值时对应的x值。
下面的例子中$min(f(x))=-2, argmin_x(f(x))=4.9$
$\textrm{if }k=\arg\min_j\left\Vert\mathbf x_n-\mu_j\right\Vert^2$
完整的符号如下:
$$\pi_nk=\left\{\begin{array}{cl}1 \;\;\; \textrm{if }k=\arg\min_j\left\Vert\mathbf x_n-\mu_j\right\Vert^2\\0 \;\textrm{otherwise}\end{array}\right.$$
这是sk-learn库算法中出现的符号,
$x_n$是已知的,并且依赖于$\pi_nk$,而如果k等于j,这个j使得$\left\Vert\mathbf x_n-\mu_j\right\Vert^2$在所有的$\mu_j$和给定的$x_n$中取得最小值,那么$\pi_nk=1$,否则就为0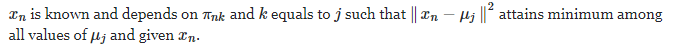

机器学习数学知识中令人费解的notation符号注解的更多相关文章
- HTML5中手势原理分析与数学知识的实践
摘要:在这触控屏的时代,人性化的手势操作已经深入了我们生活的每个部分.现代应用越来越重视与用户的交互及体验,手势是最直接且最为有效的交互方式,一个好的手势交互,能降低用户的使用成本和流程,大大提高了用 ...
- latex:数学式中的省略符号
数学式中有很多省略符号,具体命令符号和用法如下 数学式中的省略符号 \cdots 水平位置与减号等高,例如$-\cdots +$,得到- … + \ddots 对角省略号,例如$A\ddots M$, ...
- Machine Learning Algorithms Study Notes(6)—遗忘的数学知识
机器学习中遗忘的数学知识 最大似然估计( Maximum likelihood ) 最大似然估计,也称为最大概似估计,是一种统计方法,它用来求一个样本集的相关概率密度函数的参数.这个方法最早是遗传学家 ...
- 《DirectX 9.0 3D游戏开发编程基础》必备的数学知识 读书笔记
最近在看游戏导航源码,但是看了几天感觉看不懂.里面全是一些几何运算,以及一些关于3d方面的知识.发现自己缺少3d这方面的知识,正好也想研究一下3d游戏开发的基本原理,于是决定买本书看看了,后来在ope ...
- Rightmost Digit(快速幂+数学知识OR位运算) 分类: 数学 2015-07-03 14:56 4人阅读 评论(0) 收藏
C - Rightmost Digit Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit ...
- codeforces#253 D - Andrey and Problem里的数学知识
这道题是这种,给主人公一堆事件的成功概率,他仅仅想恰好成功一件. 于是,问题来了,他要选择哪些事件去做,才干使他的想法实现的概率最大. 我的第一个想法是枚举,枚举的话我想到用dfs,但是认为太麻烦. ...
- Directx11学习笔记【五】 基本的数学知识----向量篇
本文参考dx11龙书 Chapter1 vector algebra(向量代数) 要想学好游戏编程,扎实的数学知识是尤为重要的,下面将对dx11龙书中有关向量的数学知识做一下总结. 在数学中,几何向量 ...
- 机器学习数学|微积分梯度jensen不等式
机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 索引 微积分,梯度和Jensen不等式 Tay ...
- 机器学习数学|Taylor展开式与拟牛顿
机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 Taylor 展式与拟牛顿 索引 taylor ...
随机推荐
- tensorflow summary
定义summary writer = tf.summary.FileWriter(logdir=self.han_config.log_path, graph=session.graph) 1.sca ...
- alloca() 是什么?为什么不提倡使用它?
在调用 alloca() 的函数返回的时候, 它分配的内存会自动释放.也就是说, 用 alloca 分配的内存在某种程度上局部于函数的 ``堆栈帧" 或上下文中. alloca() 不具可 ...
- 在你的 Rails App 中开启 ETag 加速页面载入同时节省资源
转自http://huacnlee.com/blog/use-etag-in-your-rails-app-to-speed-up-loading/ 什么是 ETag 网上关于 ETag 的解释有很多 ...
- Feign性能优化注意事项--超时
Caused by: java.lang.IllegalStateException: PathVariable annotation was empty on param 1. at feign ...
- 17.async 函数
async 函数 async 函数 含义 ES2017 标准引入了 async 函数,使得异步操作变得更加方便. async 函数是什么?一句话,它就是 Generator 函数的语法糖. 前文有一个 ...
- Xamarin学习
慧都视频:http://training.evget.com/video/5384 极客学院视频:http://www.jikexueyuan.com/course/364.html
- c#基础学习(0719)之异常处理
异常处理的一般代码模式 try { //可能发生异常的代码 //当try中某行代码发生异常后,从该行代码开始,后面的代码都不会继续执行, //程序直接跳转到catch块中进行执行 } catch (E ...
- TFS Negotiate方式登录的IIS配置
使用vsts-agent连接到tfs(tfs2017)配置代理客户端,可以通过PAT.Negotiate.Integrated.Alternate四种方式登录.(参考) 默认情况下,采用Negotia ...
- SSH框架搭建步骤总结以及Hibernate二级缓存,查询缓存
二级缓存.查询缓存 一级缓存: 默认启动,生命周期是和session同步的,session独享 二级缓存: 需要加载配置信息,生命周期是和应用服务器同步,session共享 1:在hibernate. ...
- IOS中微信摇一摇声音无法播放解决办法
在IOS中第一次调用play方法播放音频会被阻止,必须得等用户有交互动作,比如touchstart,click后才能正常调用,所以可以在摇一摇之前提醒用户点击一下开始游戏的按钮或者给用户一个弹窗,用户 ...
