2017 国庆湖南 Day5

期望得分：76+80+30=186

实际得分：72+10+0=82

先看第一问：

本题不是求方案数，所以我们不关心 选的数是什么以及的选的顺序

只关心选了某个数后，对当前gcd的影响

预处理

cnt[i] 表示 i的倍数有多少个

g[i][j] 表示gcd（i，第j张卡片上的数）

dp[i][j] 表示已经选了i个数，gcd=j 的 概率

再选k，要么gcd不变，要么变小

1、gcd不变

即k是j的倍数，因为已经选了i个且都是j的倍数，所以在剩下的n-i 个数中，还有 cnt[j]-i 个数可以选

所以状态转移方程：dp[i+1][j]+=dp[i][j]*(cnt[j]-i)/(n-i)

2、gcd变小

枚举要选的是第h个数 ，h满足gcd（a[h]，j）！=j

（a[h] 表示第h张卡片上的数）

那么gcd会变为g[j][h]

因为 当gcd=1 的时候游戏结束，即 gcd=1 不能用来转移

所以 当gcd=1时，直接累计进答案，不更新dp

所以状态转移方程：dp[i+1][g[j][h]+=dp[i][j]/(n-i),g[j][h]!=1

答案的累计：

1、dp 过程中 gcd=1

只有 选了偶数个数之后，gcd=1，先手才赢

所以 在dp过程中，若i是奇数，ans+=dp[i][j]/(n-i)

（因为是在由i推出去的时候 累计答案，所以i是奇数）

2、dp完之后，没有牌选了

若n是奇数，则先手胜

所以若n是奇数，ans+=dp[n][i]

第二问：

就是裸地SG函数

sg[i][j] 表示 已经选了i个数，gcd=j 是必胜态（1）还是必败态（0）

根据

必胜态的后继状态至少有一个是必败态

必败态的后继状态全是必胜态

用 & 运算符可以方便的记录

记忆化搜索

边界：sg[n][i]=0,sg[i][1]=1

因为 选了n个数且j！=1 之后，对方败

当gcd=1 之后，对方胜

为什么要用对方的状态？（以下可能表述不清）

因为边界是在dfs 最前面判断的，而且是从选了0张牌开始

己方选了x张牌之后的状态，随dfs到了下一层里，即到了对方选的哪儿

如果己方选了n张牌且gcd！=1，己方赢，但sg[n][]的状态是到下一层dfs里判断的

主客交换，对方输，所以sg[n][]=0

sg[i][1] 同理

#include<cstdio>
#include<cstring>
#include<algorithm>

#define N 301
#define K 1001

using namespace std;

const double eps=1e-;

int n,m,a[N];

int cnt[K],g[K][N];

double dp[N][K];

int sg[N][K];

int getgcd(int a,int b) { return !b ? a : getgcd(b,a%b); }

void init()
{
    scanf("%d",&n);
    for(int i=;i<=n;i++) scanf("%d",&a[i]),m=max(m,a[i]);
}

void pre()
{
    for(int i=;i<=n;i++) g[][i]=a[i];
    for(int i=;i<=m;i++)
        for(int j=;j<=n;j++)
            cnt[i]+=(a[j]%i==),g[i][j]=getgcd(i,a[j]);
}

void getprobability()
{
    double ans=0.0;
    dp[][]=1.0;
    for(int i=;i<n;i++)
        for(int j=;j<=m;j++)
            if(dp[i][j]>eps)
            {
                dp[i+][j]+=dp[i][j]*(cnt[j]-i)/(n-i);
                for(int k=;k<=n;k++)
                    if(g[j][k]!=j)
                    {
                        if(g[j][k]!=) dp[i+][g[j][k]]+=dp[i][j]/(n-i);
                        else ans+=(i&)*dp[i][j]/(n-i);
                    }
            }
    if(n&)
        for(int i=;i<=m;i++) ans+=dp[n][i];
    printf("%.9lf",ans);
}

int dfs(int x,int gcd)
{
    if(sg[x][gcd]!=-) return sg[x][gcd];
    bool win=true;
    if(cnt[gcd]>x) win&=dfs(x+,gcd);
    for(int i=;i<=n;i++)
        if(g[gcd][i]!=gcd) win&=dfs(x+,g[gcd][i]);
    return sg[x][gcd]=!win;
}

void getsg()
{
    memset(sg,-,sizeof(sg));
    for(int i=;i<=m;i++) sg[n][i]=;
    for(int i=;i<=n;i++) sg[i][]=;
    if(dfs(,)) printf("1.000000000");
    else printf("0.000000000");
}

int main()
{
    freopen("cards.in","r",stdin);
    freopen("cards.out","w",stdout);
    init();
    pre();
    getprobability();
    printf(" ");
    getsg();
}

80分暴力：

删边转化成倒着加边

每次 加一条边，两个端点重新做树形DP，得到合并之后的树的权值

用并查集维护连通块

一个连通块就是一棵树，答案就是所有 连通块的权值的乘积

维护乘积 乘一下再除一下就好了，考场上智商全掉了 用的线段树

100分做法：

上述做法慢就慢在每次加一条边，两个端点重新做树形DP

这里有一个结论：

设树S1最大权值路径的两端点为u1，u2

设树S2最大权值路径的两端点为v1，v2

那么树S1和树S2合并之后

最大权值路径的两端点一定是u1,u2，v1，v2中的两个

结论的简单证明：

设合并之后的最大权值路径的两端点为k1、k2

1、k1、k2 = u1、u2  或 k1、k2=v1、v2 ，显然成立

2、k1 = u1或u2，k2=v1或v2

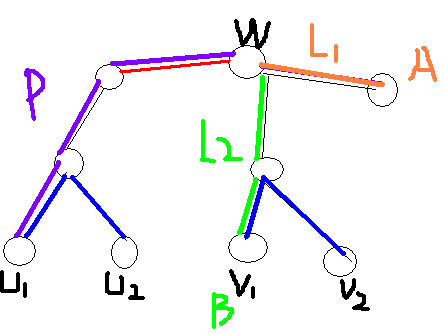
如下图所示

若选的最长权值路径为路径P+路径L1

根据dfs求树的直径的原理可推得，

w——v1 和 w——v2 中必有一条是从w出发的最大权值路径

假设是w——v1

那么选路径P+路径L2 更优

有了上述结论

那么我们每次合并只需要计算4条路径 、原来两棵树 的权值取最大

我么需要维护

val[i] 表示 当前i号连通块（树） 的最大权值

endpoint[i][2] 表示 i号连通块对应val[i] 的两端点

每次用最大的路径来更新这两个数组

每次的答案=原答案/val[S1]/val[S2]*合并之后的最大权值

如何计算路径权值？

dfs 一遍记录树上前缀和len[]

dis(u,v)=len[u]+len[v]-len[lca]+lca的权值

#include<cstdio>
#include<iostream>
#include<algorithm> 

using namespace std;

#define N 100001

const int mod=1e9+;

int n,cnt;
int cut[N],e[N][];

int front[N],to[N<<],nxt[N<<],tot;

int len[N],id[N];
int fa[N][];

int a[N],val[N],ans[N];
int endpoint[N][];

int F[N];

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar();  }
}

void add(int u,int v)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot;
}

void init()
{
    read(n); ans[n]=;
    for(int i=;i<=n;i++)
    {
        read(val[i]);
        ans[n]=1ll*ans[n]*val[i]%mod;
        endpoint[i][]=endpoint[i][]=i;
        F[i]=i; a[i]=val[i];
    }
    int u,v;
    for(int i=;i<n;i++)
    {
        read(u); read(v);
        add(u,v);
        e[i][]=u; e[i][]=v;
    }
    for(int i=;i<n;i++) read(cut[i]);
}

void dfs(int x,int f)
{
    fa[x][]=f;
    len[x]=len[f]+a[x];
    id[x]=++cnt;
    for(int i=front[x];i;i=nxt[i])
        if(to[i]!=f) dfs(to[i],x);
}

void prelca()
{
    for(int j=;j<;++j)
        for(int i=;i<=n;i++)
            fa[i][j]=fa[fa[i][j-]][j-];
}

int getlca(int u,int v)
{
    if(id[u]<id[v]) swap(u,v);
    for(int i=;i>=;i--)
        if(id[fa[u][i]]>id[v]) u=fa[u][i];
    return fa[u][];
}

int getlength(int u,int v)
{
    int lca=getlca(u,v);
    return len[u]+len[v]-*len[lca]+a[lca];
}

int find(int i) { return F[i]==i ? i : F[i]=find(F[i]); }

int Pow(int a,int b)
{
    int res=;
    for(;b;a=1ll*a*a%mod,b>>=)
        if(b&) res=1ll*res*a%mod;
    return res;
}

void solve()
{
    int u,v; int product=ans[n],mx;
    int l,e1,e2;
    for(int i=n-;i;i--)
    {
        u=e[cut[i]][],v=e[cut[i]][];
        u=find(u); v=find(v);
        if(val[u]>val[v]) mx=val[u], e1=endpoint[u][], e2=endpoint[u][];
        else mx=val[v], e1=endpoint[v][], e2=endpoint[v][];
        for(int j=;j<;j++)
            for(int k=;k<;k++)
            {
                l=getlength(endpoint[u][j],endpoint[v][k]);
                if(l>mx)
                {
                    mx=l;
                    e1=endpoint[u][j]; e2=endpoint[v][k];
                }
            }
        product=1ll*product*Pow(val[u],mod-)%mod;
        product=1ll*product*Pow(val[v],mod-)%mod;
        product=1ll*product*mx%mod;
        ans[i]=product;
        F[u]=F[v];
        endpoint[v][]=e1,endpoint[v][]=e2;
        val[v]=mx;
    }
    for(int i=;i<=n;i++) printf("%d\n",ans[i]);
}

int main()
{
    freopen("forest.in","r",stdin);
    freopen("forest.out","w",stdout);
    init();
    dfs(,);
    prelca();
    solve();
}

80分暴力

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

#define N 100001

#define lowbit(x) x&-x

const int mod=1e9+;

int val[N],e[N][],cut[N];

int front[N],to[N<<],nxt[N<<];

int tmp,tot,n;

int f[N][],out[N];

int F[N];

int st[],ans1,ans2;

int g[N<<];

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

void add(int u,int v)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot;
}

void build(int k,int l,int r)
{
    g[k]=val[l];
    if(l==r) return;
    int mid=l+r>>;
    build(k<<,l,mid); build(k<<|,mid+,r);
    g[k]=1ll*g[k<<]*g[k<<|]%mod;
}

void change(int k,int l,int r,int pos,int w)
{
    if(l==r) { g[k]=w; return; }
    int mid=l+r>>;
    if(pos<=mid) change(k<<,l,mid,pos,w);
    else change(k<<|,mid+,r,pos,w);
    g[k]=;
    if(g[k<<]!=-) g[k]=1ll*g[k]*g[k<<]%mod;
    if(g[k<<|]!=-) g[k]=1ll*g[k]*g[k<<|]%mod;
}

void init()
{
    read(n); int m1=,m2=; out[n]=;
    for(int i=;i<=n;i++)
    {
        read(val[i]); out[n]=1ll*out[n]*val[i]%mod;
        F[i]=i;
        if(val[i]>=m1) m2=m1,m1=val[i];
        else if(val[i]>m2) m2=val[i];
    }
    int u,v;
    for(int i=;i<n;i++) read(e[i][]),read(e[i][]);
    for(int i=;i<n;i++) read(cut[i]);
    build(,,n);
}

void dfs(int x,int fa)
{
    bool leave=true;
    for(int i=front[x];i;i=nxt[i])
        if(to[i]!=fa)
        {
            leave=false;
            dfs(to[i],x);
            if(f[to[i]][]>=f[x][]) f[x][]=f[x][],f[x][]=f[to[i]][];
            else if(f[to[i]][]>f[x][]) f[x][]=f[to[i]][];
            f[to[i]][]=f[to[i]][]=;
        }
    f[x][]+=val[x];
    tmp=max(tmp,f[x][]+f[x][]);
    if(!leave) f[x][]+=val[x];
}

int find(int i) { return F[i]==i ? i : F[i]=find(F[i]); }

void solve()
{
    int res1,res2,res;
    int u,v;
    for(int i=n-;i;i--)
    {
        u=e[cut[i]][]; v=e[cut[i]][];
        res=;
        tmp=; dfs(u,); res=max(res,tmp); res1=f[u][]; f[u][]=f[u][]=;
        tmp=; dfs(v,); res=max(res,tmp); res2=f[v][]; f[v][]=f[v][]=;
        change(,,n,find(v),-); F[find(v)]=find(u);
        change(,,n,F[u],max(res,res1+res2));
        out[i]=g[];
        add(u,v);
    }
    for(int i=;i<=n;i++) printf("%d\n",out[i]);
}

int main()
{
    freopen("forest.in","r",stdin);
    freopen("forest.out","w",stdout);
    init();
    solve();
}

std：

# include<iostream>
# include<cstdio>
# include<cstring>
# include<cstdlib>
using namespace std;
const int pp=;
int c[][],f[],p[],ni[];
int n,m,k,nn;
inline int power(int x,int n)
{
    int ans=,tmp=x;
    while (n)
    {
          if (n&) ans=(long long)ans*tmp%pp;
          tmp=(long long)tmp*tmp%pp;n>>=;
    }
    return ans;
}
void Count_c()
{
     for (int i=;i<=nn;i++) c[i][]=;
     for (int i=;i<=nn;i++)
      for (int j=;j<=i;j++)
      {
          c[i][j]=c[i-][j-]+c[i-][j];
          if (c[i][j]>=pp) c[i][j]-=pp;
      }
}
void Count_p()
{
     int mm=(m-)*n;
     for (int i=;i<=nn;i++)
      p[i]=power(i,mm);
}
void Count_f()
{
     f[]=;f[]=;
     for (int i=;i<=nn;i++)
     {
         f[i]=power(i,n);
         for (int j=;j<i;j++)
         {
             f[i]-=(long long)f[j]*c[i][j]%pp;
             if (f[i]<=-pp) f[i]+=pp;
         }
         if (f[i]<) f[i]+=pp;
     }
}
void Count_ni()
{
     ni[]=;
     for (int i=;i<=nn;i++)
     ni[i]=power(i,pp-);
}
int main()
{
    freopen("photo.in","r",stdin);
    freopen("photo.out","w",stdout);
    scanf("%d%d%d",&n,&m,&k);
    nn=min(n,k);
    if (m==)
       printf("%d\n",power(k,n));
    else
    {
        Count_c();
        Count_p();
        Count_f();
        Count_ni();
        long long tmp=,tmp1=,sum=,sum1;
        for (int s=;s<=nn;s++)
        {
            tmp=tmp*ni[s]%pp;
            tmp=tmp*(k-s+)%pp;
            tmp1=;sum1=;
            for (int j=;j<=s;j++)
            {
                sum1+=tmp1*c[s][s-j]%pp*p[s-j]%pp;
                if (sum1>=pp) sum1-=pp;
                tmp1=tmp1*ni[j+]%pp;
                if (k-s<j+) break;
                tmp1=tmp1*(k-s-j)%pp;
            }
            sum+=tmp*f[s]%pp*f[s]%pp*sum1%pp;
            if (sum>=pp) sum-=pp;
        }
        printf("%d\n",sum);
    }
    fclose(stdin);
    fclose(stdout);
    return ;
}