3.1 基本几何形状

球体（SphereGeometry）

构造函数：

THREE.SphereGeometry(radius, segmentsWidth, segmentsHeight, phiStart, phiLength, thetaStart, thetaLength)

radius：是半径；

segmentsWidth：经度上的切片数，相当于经度被切成了几瓣；

segmentsHeight：纬度上的切片数，相当于纬度被切成了几层；

phiStart：经度开始的弧度；

phiLength：经度跨过的弧度；

thetaStart：纬度开始的弧度；

thetaLength：纬度跨过的弧度。

分段

在图形底层的实现中，并没有曲线的概念，曲线都是由多个折线近似构成的。当折线越多，越近乎曲线。切片数决定了，图形的“精细度”

经度分段（切片demo）

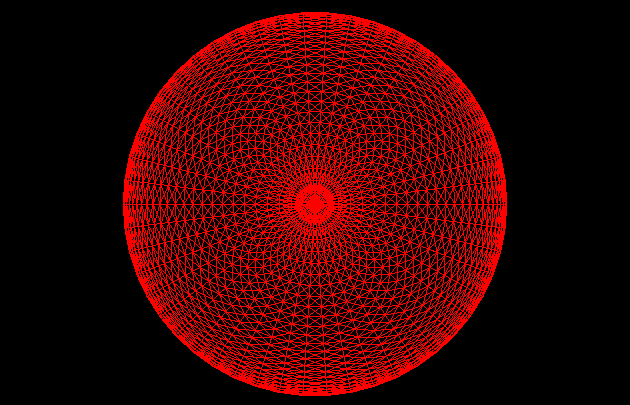
维度分段（切片demo）

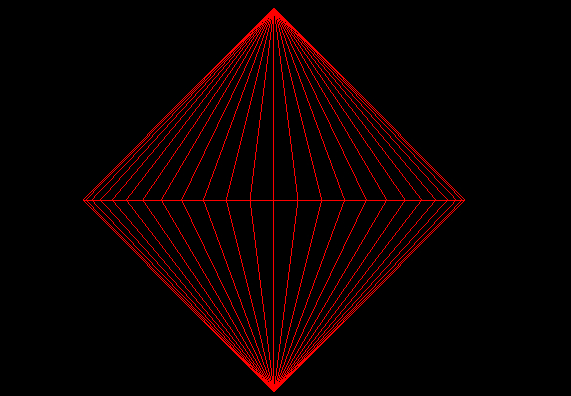
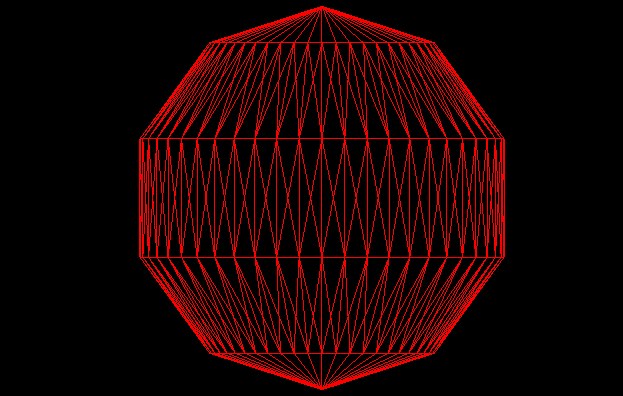
缺省值说明

phiStart、phiLength、thetaStart、thetaLength 这四个值是缺省值，即可以省略，而省略的时候实际有默认值，将画出一个完整的球体。通过不同的值修改，可以实现各种，不完整球体、球面。

例如：

THREE.SphereGeometry(2, 50, 50, Math.PI / 2, Math.PI)

（1/4 个球面）

球体的完整示例demo与效果：

<!DOCTYPE html>

<html lang="en">

<head>

    <meta charset="UTF-8">

    <meta name="viewport" content="width=device-width, initial-scale=1.0">

    <meta http-equiv="X-UA-Compatible" content="ie=edge">

    <script type="text/javascript" src="./three.js"></script>

    <title>Document</title>

</head>

<body onload="init()">

    <canvas id="mainCanvas" width="800px" height="600px"></canvas>

</body>

<script>

    function init() {

        var renderer = new THREE.WebGLRenderer({

            canvas: document.getElementById('mainCanvas')

        });

        renderer.setClearColor(0x000000);

        var scene = new THREE.Scene();

        var aspect = window.innerWidth / window.innerHeight;

        var camera = new THREE.OrthographicCamera(-2 * aspect, 2 * aspect, -1.5 * aspect, 1.5 * aspect, 1, 500);

        camera.position.set(200, 200, 200);

        scene.add(camera);

        camera.lookAt(new THREE.Vector3(0, 0, 0));

        var cube = new THREE.Mesh(new THREE.SphereGeometry(2, 50, 50),

            new THREE.MeshBasicMaterial({

                color: 0xff0000,

                wireframe: true

            })

        )

        scene.add(cube);

        renderer.render(scene, camera);

    }

</script>

</html>

　　

《Three.js 入门指南》3.1.1 - 基本几何形状 - 球体（SphereGeometry）的更多相关文章

  1. d3.js 入门指南 - 仪表盘

    D3的全称是Data-Driven Documents(数据驱动的文档),是一个用来做数据可视化的JavaScript函数库,而JavaScript文件的后缀通常为.js,所以D3被称为D3.js. ...

  2. d3.js 入门指南

    说到数据可视化,我们会行到很多优秀的框架,像echarts.highcharts,这些框架很优雅,健壮,能满足我们对可视化的大部分需求,但是缺点也很明显,就是这些框架几乎是不可定制化的,当遇到特殊的需 ...

  3. 《Three.js 入门指南》3.1.2 - 一份整齐的代码结构以及使用ORBIT CONTROLS插件（轨道控制）实现模型控制

    3.1.2 正式代码结构 & ORBIT CONTROLS插件(轨道控制) 说明 本节内容属于插入节,<Three.js入门指南>这本书中,只是简单的介绍了一些概念,是一本基础的入 ...

  4. 《Three.js 入门指南》3.0 - 代码构建的最基本结构。

    3.0 代码构建的最基本结构 说明: 我们必需首先知道,Three.js 的一些入门级概念: 我们需要知道,OpenGL 是一套三维实现的标准,为什么说是标准,因为它是跨平台,跨语言的.甚至CAD以及 ...

  5. 《Three.js 入门指南》0 - 说明

    本笔记,摘自:<Three.js 入门指南>一书 地址链接为:https://www.ituring.com.cn/book/miniarticle/58552 本书的前言摘录: 本书结构 ...

  6. Vue.js 入门指南之“前传”（含sublime text 3 配置）

    题记:关注Vue.js 很久了,但就是没有动手写过一行代码,今天准备入手,却发现自己比菜鸟还菜,于是四方寻找大牛指点,才终于找到了入门的“入门”,就算是“入门指南”的“前传”吧.此文献给跟我一样“白痴 ...

  7. 系列博文-Three.js入门指南(张雯莉)-静态demo和three.js功能概览

    一:一个最简单的静态DEMO //body加载完后触发init() //WebGL的渲染是需要HTML5 Canvas元素的,你可以手动在HTML的<body>部分中定义Canvas元素, ...

  8. 《Three.js 入门指南》3.1.1 - 基本几何形状 -圆环结（TorusKnotGeometry）

    3.1 基本几何形状 圆环结(TorusKnotGeometry) 构造函数 THREE.TorusKnotGeometry(radius, tube, radialSegments, tubular ...

  9. 《Three.js 入门指南》3.1.1 - 基本几何形状 -圆环面（TorusGeometry）

    3.1 基本几何形状 圆环面(TorusGeometry) 构造函数 THREE.TorusGeometry(radius, tube, radialSegments, tubularSegments ...

随机推荐

  1. javascript设计模式和开发实践（阶段一）

    1,设计模式的作用:让人们写出可复用和可维护性高的程序,代价可能是,额外增加代码量: 比较形象的例子:空房间里面放东西,如果日复一日的往里面扔东西,时间久了,很难找到自己想要的东西,调整也不容易,但是 ...

  2. 2020ubuntu1804server编译安装redis笔记（三）启动服务和使用redis

    第一篇笔记记录了ubuntu1804server编译安装redis5,接下来要配置redis5了 网址:https://www.cnblogs.com/qumogu/p/12435694.html 第 ...

  3. 打造你的第一个 Electron 应用

    Electron 可以让你使用纯 JavaScript 调用丰富的原生(操作系统) APIs 来创造桌面应用. 你可以把它看作一个 Node. js 的变体,它专注于桌面应用而不是 Web 服务器端. ...

  4. can do / will do / should do 情态动词

    can do = be able to do will do = be going to do should do = ought to do 情态动词 都是表示建议 从这里发现 to do (不确定 ...

  5. java实现简单的星座查询

    在校小白,大神勿喷. 版本已简化 连接mysql数据库验证用户名及密码进行登陆 public class mysql {Connection con;public mysql(){    try{   ...

  6. java-3个例子（新手）

    //创建的一个包名. package ri0318; //创建的一个类. public class Li3 { //公共静态的主方法. public static void main(String[] ...

  7. 面向对象第四单元(UML)及期末总结

    前言 统一建模语言(英语:Unified Modeling Language,缩写 UML),是软件架构设计建模和规约的语言. 在UML系统开发中有三个主要的模型: 功能模型:从用户的角度展示系统的功 ...

  8. 微信小程序校历组件

    微信小程序校历组件 校历组件,可以作为校园小程序的插件,如果觉得不错,点个star吧

  9. no parameterless constructor define for type 解决一例

    在生成根据模型和上下文生成带增删查改操作的视图的控制器时,提示上述信息,网上查找了资料也没有解决,突然想起该项目是连接MSSQL数据库和Redis数据库的,并且已经依赖注入了,而Redis数据库的服务 ...

  10. 动态规划-区间dp-Palindrome Removal

    2019-11-09 10:31:09 问题描述: 问题求解: n = 100,典型的O(n ^ 3)的动规问题.一般来说这种O(n ^ 3)的问题可以考虑使用区间dp来解决. 区间dp是典型的三层结 ...