神经网路的层数,损失函数(loss)
神经网络的复杂度:可用神经网络的层数和神经网络中待优化参数个数表示
神经网路的层数:一般不计入输入层,层数 = n 个隐藏层 + 1 个输出层
神经网路待优化的参数:神经网络中所有参数 w 的个数 + 所有参数 b 的个数
如:
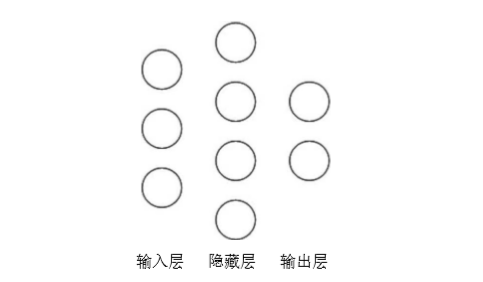
在该神经网络中,包含 1 个输入层、1 个隐藏层和 1 个输出层,该神经网络的层数为 2 层。
在该神经网络中,参数的个数是所有参数 w 的个数加上所有参数 b 的总数,第一层参数用三行四列的二阶张量表示(即 12 个线上的权重 w)再加上 4 个偏置 b;
第二层参数是四行两列的二阶张量()即8 个线上的权重 w)再加上 2 个偏置 b。总参数 = 3*4+4 + 4*2+2 = 26。
损失函数(loss): 用来表示预测值(y)与已知答案(y_)的差距。在训练神经网络时,通过不断改变神经网络中所有参数,使损失函数不断减小,从而训练出更高准确率的神经网络模型。
常用的损失函数有均方误差、自定义和交叉熵等。
均方误差 mse:n 个样本的预测值 y 与已知答案 y_之差的平方和,再求平均值。 在 Tensorflow 中用 loss_mse = tf.reduce_mean(tf.square(y_ - y))
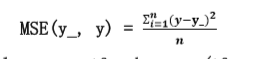
神经网路的层数,损失函数(loss)的更多相关文章
- 人工智能起步-反向回馈神经网路算法(BP算法)
人工智能分为强人工,弱人工. 弱人工智能就包括我们常用的语音识别,图像识别等,或者为了某一个固定目标实现的人工算法,如:下围棋,游戏的AI,聊天机器人,阿尔法狗等. 强人工智能目前只是一个幻想,就是自 ...
- 机器学习 损失函数(Loss/Error Function)、代价函数(Cost Function)和目标函数(Objective function)
损失函数(Loss/Error Function): 计算单个训练集的误差,例如:欧氏距离,交叉熵,对比损失,合页损失 代价函数(Cost Function): 计算整个训练集所有损失之和的平均值 至 ...
- 损失函数(Loss function) 和 代价函数(Cost function)
1损失函数和代价函数的区别: 损失函数(Loss function):指单个训练样本进行预测的结果与实际结果的误差. 代价函数(Cost function):整个训练集,所有样本误差总和(所有损失函数 ...
- 损失函数(Loss Function) -1
http://www.ics.uci.edu/~dramanan/teaching/ics273a_winter08/lectures/lecture14.pdf Loss Function 损失函数 ...
- 损失函数(loss function) 转
原文:http://luowei828.blog.163.com/blog/static/310312042013101401524824 通常而言,损失函数由损失项(loss term)和正则项(r ...
- tensorflow学习2-线性拟合和神经网路拟合
线性拟合的思路: 线性拟合代码: import tensorflow as tf import numpy as np import matplotlib.pyplot as plt #%%图形绘制 ...
- 损失函数(loss function)
通常而言,损失函数由损失项(loss term)和正则项(regularization term)组成.发现一份不错的介绍资料: http://www.ics.uci.edu/~dramanan/te ...
- 神经网路-SGD-1
SGD神经网络以及python中实现 1.SGD(stochastic gradient descend):<1>数据抽取:<2>计算梯度;<3>参数更新:< ...
- tensorflow学习之路-----简单卷积神经网路
import tensorflow as tf#取数据,目的是辨别数字from tensorflow.examples.tutorials.mnist import input_data'''手动添加 ...
随机推荐
- 《剑指Offer》各面试题总结
目录 前言 面试题4 二维数组的查找 面试题5:替换空格 面试题6:从尾到头打印链表 面试题7:重建二叉树 面试题8:二叉树的下一个节点 面试题9:用两个栈实现队列 面试题10:斐波那契数列 面试题1 ...
- 记录 Docker 的学习过程 (网络篇之跨主机互通)
下面从node3上操作node3# docker run -d -p 8500:8500 --name consul progrium/consul -server -bootstrap node3# ...
- Mariadb Galera Cluster 搭建集群
1.安装MariaDB 和Galera 见另外一篇博客 2.环境修改 2.1 防火墙和SELinux 这里不做说明,参照网上教程,和官方的配置 2.2. 创建用于节点同步的账号 [root@local ...
- nginx 部署php项目 404
服务器重启了一下 然后访问程序报错404的情况 文件存在位置没有问题 niginx配置根目录没有问题 最后检查到端口的时候发现php-fpm的9000端口未打开 service php-fpm res ...
- 一步步教你如何在ubuntu虚拟机中安装QEMU并模拟arm 开发环境(二)rootfs制作
过了,一天,周又到了,博主终于可以拿出时间来把上一次没有给大家展示完了的内容今天在这里一并展示给大家,希望和大家共同进步,共同学习,同时我也虔诚的希望各位业界的朋友把自己的工作经验拿出来大家一起分享, ...
- centos7下编译安装redis5.05
准备环境: 1.一台centos7机器,配置没有什么要求(能联网) 2.下载好redis压缩包 下载redis包: 1.登录redis官网: https://redis.io/download 2.选 ...
- X shell安装 以及使用
X shell 百度搜索 X shell 然后下载软件 然后会进入主页面
- 导入org.apache.poi.xssf 读取excel
POI 操作 excel 用XSSF 方式时,如果不能自动导入 org.apache.poi.xssf 对应jar 包,则可以Apache 官网进行下载,自行导入. step1: 访问 http:/ ...
- Winfrom控件 特效
链接:https://pan.baidu.com/s/1O9e7sxnYFYWD55Vh5fxFQg 提取码:5cey 复制这段内容后打开百度网盘手机App,操作更方便哦 Winfrom控件查询手册. ...
- 【Python】random库
种子相同,随机数相同
