Educational Codeforces Round 7 F - The Sum of the k-th Powers 拉格朗日插值

The Sum of the k-th Powers

There are well-known formulas: 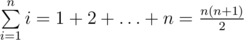, , 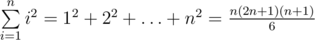. Also mathematicians found similar formulas for higher degrees.

Find the value of the sum modulo 10⁹ + 7 (so you should find the remainder after dividing the answer by the value 10⁹ + 7).

Input

The only line contains two integers n, k (1 ≤ n ≤ 10⁹, 0 ≤ k ≤ 10⁶).

Output

Print the only integer a — the remainder after dividing the value of the sum by the value 10⁹ + 7.

Examples

Input

4 1

Output

10

拉格朗日插值:本质就是通过给定函数的n个点，求未知自变量的函数值；万能公式
细节:题目中给了k前几项的n的通项公式，其中n的最高次为k + 1次；由拉格朗日插值的构造多项式知，当代入k个点时，得到的是k - 1次多项式，
所以要得到最终的k + 1次多项式就需要先求出在函数中的k+2,这样就可以按照得到的多项式代入n求出最终的结果；
  
pi就是已知点的函数值，原本得到的k + 1次多项式n是x才对，这里直接将n替换成了x,得到的就是最终的结果；因为我们知道最终的多项式的次数(关键)
实现细节: 对内层阶乘先预处理出来，但是里面并不是连续的阶乘，需要用到乘法逆元，即欧拉函数推导式；至于分母的正负，可以求完逆元之后在判断(这并没有证明)
时间复杂度:对于n小于maxn时，其实是可以直接求的，时间复杂度为O(maxn*log(maxn));但是当n接近1e9时，一定要用拉格朗日插值法，时间复杂度为O(klog(k));

#include<bits/stdc++.h>
using namespace std;
typedef __int64 ll;
const int mod = 1e9 + ;
const int maxn = 1e6 + ;
ll p[maxn],fac[maxn];
ll pow_mod(ll a,ll n)
{
    ll ans = ;
    while(n){
        if(n & ) ans = ans*a%mod;
        a = a*a%mod;
        n >>= ;
    }
    return ans;
}
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    p[] = ;
    for(int i = ;i <= k + ;i++)
        p[i] = (p[i - ] + pow_mod(i,k))%mod;
    if(n <= k + )
        return printf("%I64d",p[n]),;
    fac[] = ;
    for(int i = ;i <= k + ;i++)
        fac[i] = fac[i - ]*i%mod;
    ll t = ;
    for(int i = ;i <= k+; i++)
        t = (n - i)*t%mod;
    ll ans = ;
    for(int i = ;i <= k + ;i++){
        ll t1 = pow_mod(fac[i-]*fac[k+-i]%mod,mod - );//求解逆元
        ll t2 = pow_mod(n-i,mod - )%mod;
        if((k+-i)&) t1 = -t1;
        ans = (ans + p[i]*t%mod*t2%mod*t1%mod + mod)%mod;
    }
    cout<<ans;
}