webpack配置：css文件打包、JS压缩打包和HTML文件发布

一、CSS文件打包

　　1、在src下新建css文件，在css文件下新建index.css文件，输入以下代码

body{
    color:red;
    font-size:20px;
}

　　2、css建立好后，需要引入到入口文件，这里我们引入到index.js中

import css from './css/index.css';

document.write("It works.");

　　3、在终端安装style-loader和css-loader

　　4、安装好后，我们开始在webpack.config.js中配置module选项

//模块：例如解读CSS,图片如何转换，压缩
module:{
    rules:[
        {
            test:/\.css$/,
            use:['style-loader','css-loader']
        }
    ]
},

　　5、在终端输入 npm run server，可以看到出来的效果有了样式。

二、JS压缩打包

1、首先在webpack.config.js中引入

const uglify = require('uglifyjs-webpack-plugin');

2、然后在plugins里配置

//插件，用于生产模版和各项功能
plugins:[
    new uglify()
],//  插件，多个插件，所以是数组

const path = require('path');
const uglify = require('uglifyjs-webpack-plugin');
module.exports={
    //入口文件的配置项
    entry:{
        entry:'./src/index.js'
    },
    //出口文件的配置项
    output:{
        //输出的路径，用了Node语法
        path:path.resolve(__dirname,'dist'),
        //输出的文件名称
        filename:'bundle.js'
    },
    mode:"development",
    //模块：例如解读CSS,图片如何转换，压缩
    module:{
        rules:[
            {
                test:/\.css$/,
                use:['style-loader','css-loader']
            }
        ]
    },
    //插件，用于生产模版和各项功能
    plugins:[
        new uglify()
    ],//  插件，多个插件，所以是数组
    //配置webpack开发服务功能
    devServer:{
        contentBase:path.resolve(__dirname,'dist'),//本地服务器所加载的页面所在的目录
        host:'192.168.118.221',
        compress:true,
        port:
    }//  配置webpack服务
}

3、在终端输入webpack，你会发现JS代码已经被压缩了

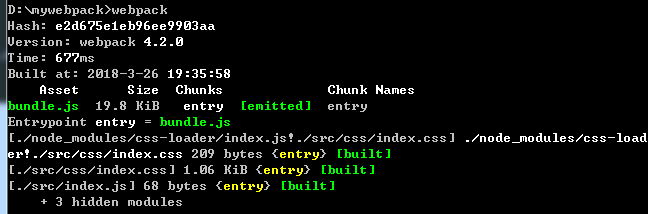
三、HTML文件发布

1、把dist中的index.html复制到src目录中，并去掉我们引入的js

2、在webpack.config.js中引入

const htmlPlugin = require('html-webpack-plugin');

3、引入后进行安装   npm install html-webpack-plugin --save-dev

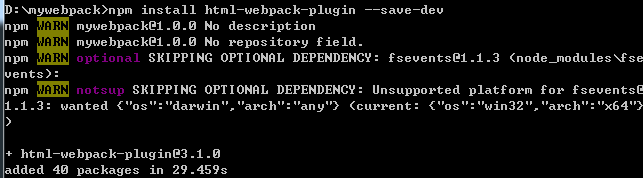
4、在webpack.config.js中进行插件配置

plugins:[
    new uglify(),
    new htmlPlugin({
        minify:{
            removeAttributeQuotes:true
        },
        hash:true,
        template:'./src/index.html'
     })
],//  插件，多个插件，所以是数组

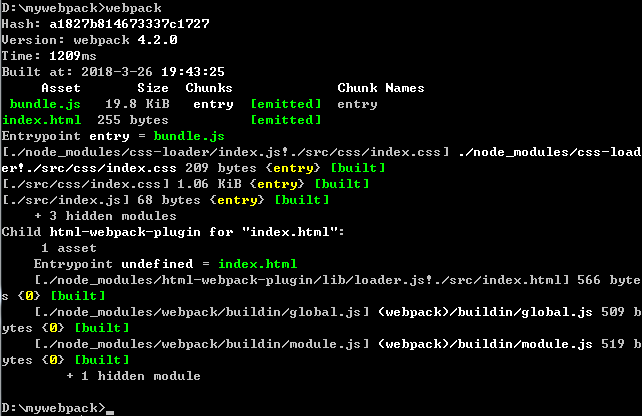
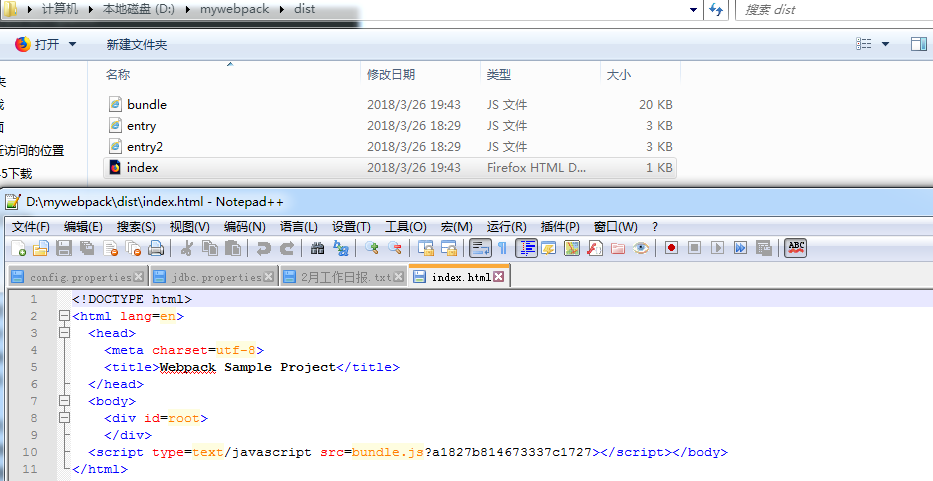
5、在终端中输入webpack，进行打包，你会看到index.html文件已经被我们打包到dist文件目录下了，并且自动引入了js文件