NOI2011真题：兔兔与蛋蛋游戏

NOI2011真题：兔兔与蛋蛋游戏

---

题目描述

这些天，兔兔和蛋蛋喜欢上了一种新的棋类游戏。

这个游戏是在一个 n行 m 列的棋盘上进行的。游戏开始之前，棋盘上有一个格子是空的，其它的格子中都放置了一枚棋子，棋子或者是黑色，或者是白色。

每一局游戏总是兔兔先操作，之后双方轮流操作，具体操作为：

·兔兔每次操作时，选择一枚与空格相邻的白色棋子，将它移进空格。

·蛋蛋每次操作时，选择一枚与空格相邻的黑色棋子，将它移进空格。

第一个不能按照规则操作的人输掉游戏。为了描述方便，下面将操作“将第x行第y列中的棋子移进空格中”记为 M(x,y)M(x,y)。

例如下面是三个游戏的例子。



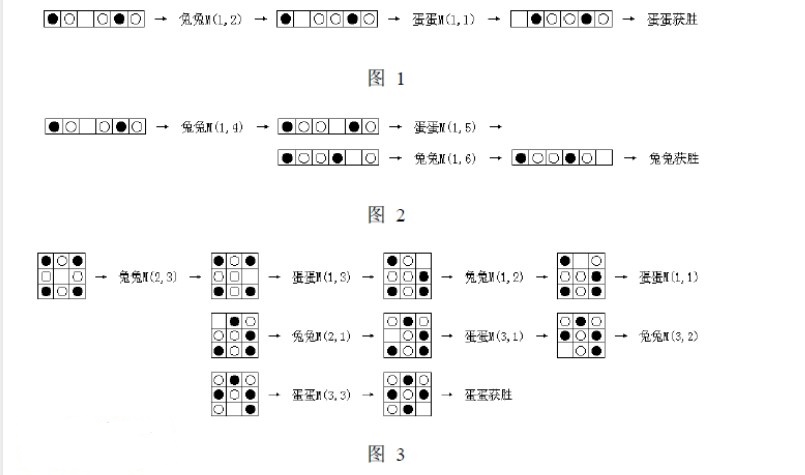
最近兔兔总是输掉游戏，而且蛋蛋格外嚣张，于是兔兔想请她的好朋友——你——来帮助她。她带来了一局输给蛋蛋的游戏的实录，请你指出这一局游戏中所有她“犯错误”的地方。

注意：

·两个格子相邻当且仅当它们有一条公共边。

·兔兔的操作是“犯错误”的，当且仅当，在这次操作前兔兔有必胜策略，而这次操作后蛋蛋有必胜策略。

输入格式

输入的第一行包含两个正整数 n,m。

接下来 n 行描述初始棋盘。其中第 i 行包含 m个字符，每个字符都是大写英文字母 X、大写英文字母 O 或点号 . 之一，分别表示对应的棋盘格中有黑色棋子、有白色棋子和没有棋子。其中点号 . 恰好出现一次。

接下来一行包含一个整数 k（1≤k≤1000） ，表示兔兔和蛋蛋各进行了 k 次操作。

接下来 2k 行描述一局游戏的过程。其中第 2i – 1 行是兔兔的第 i 次操作（编号为 i 的操作） ，第 2i 行是蛋蛋的第 i 次操作。每个操作使用两个整数 x,y 来描述，表示将第 x 行第 y列中的棋子移进空格中。

输入保证整个棋盘中只有一个格子没有棋子， 游戏过程中兔兔和蛋蛋的每个操作都是合法的，且最后蛋蛋获胜。

输出格式

输出文件的第一行包含一个整数 r，表示兔兔犯错误的总次数。

接下来 r行按递增的顺序给出兔兔“犯错误”的操作编号。其中第 i 行包含一个整数ai表示兔兔第 i 个犯错误的操作是他在游戏中的第 ai次操作。

输入样例：

1 6

XO.OXO

1

1 2

1 1

输出样例：

1

1

说明提示：

解法：

知识：二分图，博弈论，深度优先搜索

先审清楚题意。A 一步走错的判定：A 走这步之前，A先手采用最优策略必胜；A 走这步之后，B先手采用最优策略必胜。

判断的过程：强制当前点不选，如果它的匹配点仍然能找到新的匹配点，说明有一种最大匹配不包含它，自然它就不是 一定 在最大匹配中。

代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=41,MAXS=1601,MAXK=1001;
int n,m,dx[]={0,0,1,-1},dy[]={1,-1,0,0};
int tar[MAXS];
bool vis[MAXS],win[MAXK];
bool bel[MAXN][MAXN],col[MAXN][MAXN],del[MAXS];
vector <int> edge[MAXS],src;
inline int id(int x,int y) {
	if(x<1||x>n||y<1||y>m||bel[x][y]!=col[x][y]) return -1;
	return (x-1)*m+y;
}
inline bool match(int p) {
	if(del[p]) return false;
	for(int x:edge[p]) {
		if(vis[x]||del[x]) continue;
		vis[x]=true;
		if(tar[x]==-1||match(tar[x])) {
			tar[x]=p;
			return true;
		}
	}
	return false;
}
inline int MM() {
	int ret=0;
	memset(tar,-1,sizeof(tar));
	for(int x:src) {
		memset(vis,false,sizeof(vis));
		if(match(x)) ++ret;
	}
	return ret;
}
signed main() {
	int kx,ky;
	cin>>n>>m;
	for(int i=1;i<=n;++i) {
		for(int j=1;j<=m;++j) {
			char ch;
			cin>>ch;
			if(ch=='.') kx=i,ky=j,bel[i][j]=true;
			else bel[i][j]=(ch=='X');
		}
	}
	for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) col[i][j]=((i+j)%2==(kx+ky)%2);
	for(int i=1;i<=n;++i) {
		for(int j=1;j<=m;++j) {
			if(bel[i][j]&&col[i][j]) {
				src.push_back(id(i,j));
				for(int k:{0,1,2,3}) {
					int x=i+dx[k],y=j+dy[k];
					if(id(x,y)!=-1) {
						edge[id(i,j)].push_back(id(x,y));
					}
				}
			}
		}
	}
	int stdv=MM(),k;
	del[id(kx,ky)]=true;
	int tmpv=MM();
	win[1]=tmpv!=stdv;
	stdv=tmpv;
	scanf("%d",&k);
	vector <int> ans;
	for(int i=1;i<=k;++i) {
		int tx,ty;
		scanf("%d%d",&tx,&ty);
		del[id(tx,ty)]=true;
		tmpv=MM();
		win[i*2]=tmpv!=stdv;
		stdv=tmpv;
		if(win[i*2]&&win[i*2-1]) ans.push_back(i);
		scanf("%d%d",&tx,&ty);
		del[id(tx,ty)]=true;
		tmpv=MM();
		win[i*2+1]=tmpv!=stdv;
		stdv=tmpv;
	}
	printf("%d\n",(int)ans.size());
	for(int p:ans) printf("%d\n",p);
	return 0;
}