[LeetCode] 84. Largest Rectangle in Histogram 直方图中最大的矩形

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

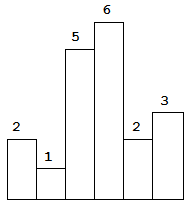
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

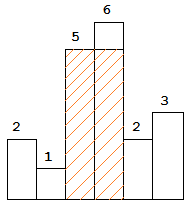
The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

这道题让求直方图中最大的矩形，刚开始看到求极值问题以为要用DP来做，可是想不出递推式，只得作罢。这道题如果用暴力搜索法估计肯定没法通过OJ，但是我也没想出好的优化方法，在网上搜到了网友水中的鱼的博客，发现他想出了一种很好的优化方法，就是遍历数组，每找到一个局部峰值（只要当前的数字大于后面的一个数字，那么当前数字就看作一个局部峰值，跟前面的数字大小无关），然后向前遍历所有的值，算出共同的矩形面积，每次对比保留最大值。这里再说下为啥要从局部峰值处理，看题目中的例子，局部峰值为 2，6，3，我们只需在这些局部峰值出进行处理，为啥不用在非局部峰值处统计呢，这是因为非局部峰值处的情况，后面的局部峰值都可以包括，比如1和5，由于局部峰值6是高于1和5的，所有1和5能组成的矩形，到6这里都能组成，并且还可以加上6本身的一部分组成更大的矩形，那么就不用费力气去再统计一个1和5处能组成的矩形了。代码如下：

解法一：

// Pruning optimize
class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int res = ;
        for (int i = ; i < height.size(); ++i) {
            if (i +  < height.size() && height[i] <= height[i + ]) {
                continue;
            }
            int minH = height[i];
            for (int j = i; j >= ; --j) {
                minH = min(minH, height[j]);
                int area = minH * (i - j + );
                res = max(res, area);
            }
        }
        return res;
    }
};

后来又在网上发现一种比较流行的解法，是利用栈来解，可参见网友实验室小纸贴校外版的博客，但是经过仔细研究，其核心思想跟上面那种剪枝的方法有异曲同工之妙，这里维护一个栈，用来保存递增序列，相当于上面那种方法的找局部峰值。我们可以看到，直方图矩形面积要最大的话，需要尽可能的使得连续的矩形多，并且最低一块的高度要高。有点像木桶原理一样，总是最低的那块板子决定桶的装水量。那么既然需要用单调栈来做，首先要考虑到底用递增栈，还是用递减栈来做。我们想啊，递增栈是维护递增的顺序，当遇到小于栈顶元素的数就开始处理，而递减栈正好相反，维护递减的顺序，当遇到大于栈顶元素的数开始处理。那么根据这道题的特点，我们需要按从高板子到低板子的顺序处理，先处理最高的板子，宽度为1，然后再处理旁边矮一些的板子，此时长度为2，因为之前的高板子可组成矮板子的矩形 ，因此我们需要一个递增栈，当遇到大的数字直接进栈，而当遇到小于栈顶元素的数字时，就要取出栈顶元素进行处理了，那取出的顺序就是从高板子到矮板子了，于是乎遇到的较小的数字只是一个触发，表示现在需要开始计算矩形面积了，为了使得最后一块板子也被处理，这里用了个小 trick，在高度数组最后面加上一个0，这样原先的最后一个板子也可以被处理了。由于栈顶元素是矩形的高度，那么关键就是求出来宽度，那么跟之前那道 Trapping Rain Water 一样，单调栈中不能放高度，而是需要放坐标。由于我们先取出栈中最高的板子，那么就可以先算出长度为1的矩形面积了，然后再取下一个板子，此时根据矮板子的高度算长度为2的矩形面积，以此类推，知道数字大于栈顶元素为止，再次进栈，巧妙的一比！关于单调栈问题可以参见博主的一篇总结帖 LeetCode Monotonous Stack Summary 单调栈小结，代码如下：

解法二：

class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int res = ;
        stack<int> st;
        height.push_back();
        for (int i = ; i < height.size(); ++i) {
            if (st.empty() || height[st.top()] < height[i]) {
                st.push(i);
            } else {
                int cur = st.top(); st.pop();
                res = max(res, height[cur] * (st.empty() ? i : (i - st.top() - )));
                --i;
            }
        }
        return res;
    }
};

我们可以将上面的方法稍作修改，使其更加简洁一些：

解法三：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int res = ;
        stack<int> st;
        heights.push_back();
        for (int i = ; i < heights.size(); ++i) {
            while (!st.empty() && heights[st.top()] >= heights[i]) {
                int cur = st.top(); st.pop();
                res = max(res, heights[cur] * (st.empty() ? i : (i - st.top() - )));
            }
            st.push(i);
        }
        return res;
    }
};

类似题目：

Maximal Square

Maximal Rectangle

参考资料：

https://leetcode.com/problems/largest-rectangle-in-histogram/

https://leetcode.com/problems/largest-rectangle-in-histogram/discuss/28905/My-concise-C%2B%2B-solution-AC-90-ms

https://leetcode.com/problems/largest-rectangle-in-histogram/discuss/28902/5ms-O(n)-Java-solution-explained-(beats-96)

LeetCode All in One 题目讲解汇总(持续更新中...)