"一起来捉妖"怎么从瘸腿中组合到最合心意的妖灵

背景：

最近两天活动，黑鬼白鬼合体觉醒秋容，陆无名，聂小倩，作为一个非土豪玩家，没有超高资质妖灵的我，想要在瘸腿妖灵中选取两个最佳选择，合体觉醒。

初选：

备选妖灵从5个维度录入数据，进行选择，分别为物攻，物防，法攻，法防，生命。事先考察，被觉醒大佬妖灵均属于法攻属性，所有法攻资质务必作为重要参考。

经过一番筛选，海选出以下黑白鬼，各五组妖灵：

	白
物攻	32	26	20	25	10
物防	21	32	24	27	27
法攻	30	24	32	28	22
法防	28	30	26	27	30
生命	27	25	32	26	32
	黑
物攻	28	27	14	21	1
物防	28	25	31	18	29
法攻	26	20	32	30	31
法防	28	31	13	28	16
生命	26	22	32	20	32

操作：

抽象化，各自五组，资质取平均，那么一共有25组组合方式，是个二维数组的笛卡尔组合，网上挺多资料处理笛卡尔积算法的。

 package tools;

 import org.slf4j.Logger;
 import org.slf4j.LoggerFactory;

 public class getBestGhost {
     private static final Logger log = LoggerFactory.getLogger(getBestGhost.class);

     public static void main(String[]args)//测试
     {
         Integer [][] TMatrix1 = {
                 {32, 21, 30,28,27},
                 {26, 32,24,30,25} ,
                 {20,24,32,26,32},
                 {25,27,28,27,26},
                 {10,27,22,30,32}
         };
         Integer [][] TMatrix2={
                 {28,28,26,28,26},
                 {27,25,20,31,22},
                 {14,31,32,13,32},
                 {21,18,30,28,20},
                 {1,29,31,16,32}
         };

         String Strr=new String("");

         for(int i=0;i<5;i++)
         {
             for(int j=0;j<5;j++)
             {
                 String str=String.valueOf(MatrixsAdds(TMatrix1,5,5,TMatrix2)[i][j]);//
                 Strr+=str;
                 Strr+=" ";
             }
             Strr+="\n";
         }
         System.out.println(Strr);
     }

     public static Integer[][] MatrixsAdds(Integer[][]A, int line, int list, Integer[][] B){
         Integer [][]C=new Integer[line][list];
         for(int i=0;i<line;i++)
         {
             for(int j=0;j<list;j++)
             {
                 //替换B数组维度，代表黑鬼，替换
                     C[i][j]=(A[i][j]+B[0][j])/2;
             }

         }
         return C;
     }
 }

得出以下结果，它们是初生的游灵，我们需要从中选择，觉醒大佬，我已经高亮了其中尚且客观的资质鬼。

一组整体平平，说明黑鬼1号资质平平拖了后腿

二组法攻整体偏短，比较是主技能，带出去打架太怂不太好，放弃2号黑鬼

三组比较突出说明3号黑鬼比较合适

 

三，四，五组每组，第三个鬼都比较突出，说明3号白鬼比较优秀

 

白1黑1	30 24 28 28 26	白1黑2	29 23 25 29 24	白1黑3	23 26 31 20 29
白2黑1	27 30 25 29 25	白2黑2	26 28 22 30 23	白2黑3	20 31 28 21 28
白3黑1	24 26 29 27 29	白3黑2	23 24 26 28 27	白3黑3	17 27 32 19 32
白4黑1	26 27 27 27 26	白4黑2	26 26 24 29 24	白4黑3	19 29 30 20 29
白5黑1	19 27 24 29 29	白5黑2	18 26 21 30 27	白5黑3	12 29 27 21 32
白1黑4	26 19 30 28 23	白1黑5	16 25 30 22 29
白2黑4	23 25 27 29 22	白2黑5	13 30 27 23 28
白3黑4	20 21 31 27 26	白3黑5	10 26 31 21 32
白4黑4	23 22 29 27 23	白4黑5	13 28 29 21 29
白5黑4	15 22 26 29 26	白5黑5	5 28 26 23 32

权衡一下，我们可以合成两只，白4黑3 和  白3黑5。

白3黑5：

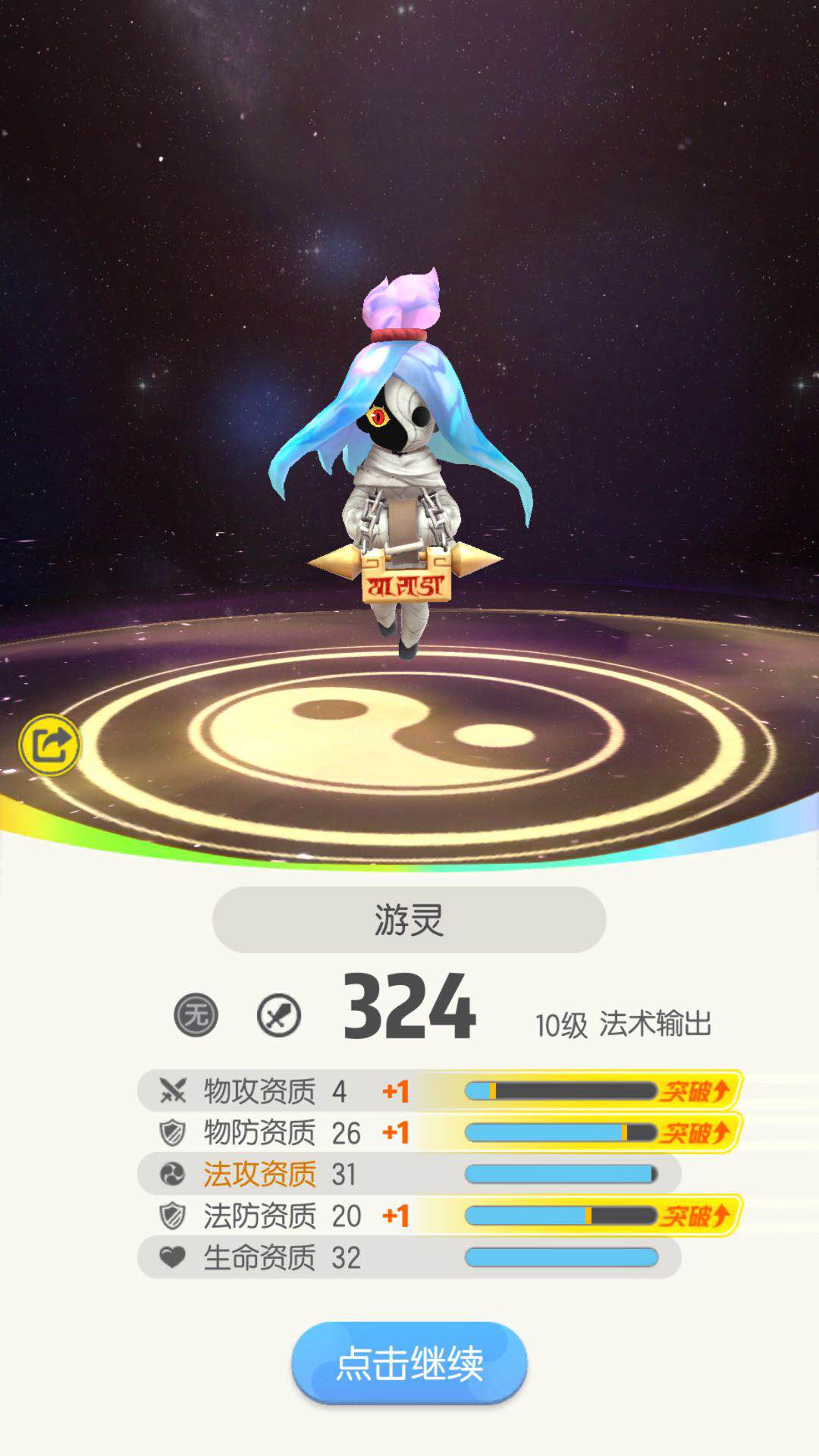
物攻资质跟我们实际分析的结果有点出入，不过不影响发挥，其他参数基本一致。