【XSY2708】hack 网络流

题目描述

　　给你一个图，每条边有一个权值。要求你选一些边，满足对于每条从\(1\)到\(n\)的路径上（可以不是简单路径）有且仅有一条被选中的边。问你选择的边的边权和最小值。

　　\(n\leq 100\)

题解

　　先把整张图分为两个集合\(S,T\)，其中\(S\)是从原点开始BFS能够到达的点组成的集合，\(T\)是剩下的点组成的集合。

　　如果没有在一条路径上只能选一条边的限制，就是一个普通的网络流了。

　　我们看看什么情况下这个条件不会被满足。

　　

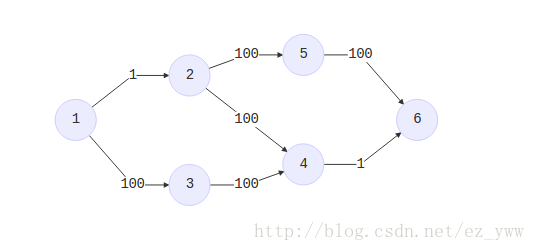
　　上面这个图中我们选择了\((1,2)\)和\((4,6)\)。\(S=\{1,3,4\},T=\{2,5,6\}\)。

　　可以发现如果多次从\(S\)走到\(T\)（比如上面这张图中\(1\rightarrow2\rightarrow4\rightarrow6\)），那么这些\(S\rightarrow T\)的边就都被选中同时在同一条路径上。所以不合法。

　　所以一旦走到\(T\)后就不能走回\(S\)。　　

　　如果一条边从\(T\)指向\(S\)，那么这条边的反向边就满流了。

　　为了避免这种情况，只需要把反向边的容量设为\(\infty\)。

　　坑点：如果一条边的两个断点与\(S\)或\(T\)不连通，就不要连边。

　　时间复杂度：\(O(\)能过\()\)

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef long long ll;
const ll inf=1e15;
namespace flow
{
	int v[100010];
	ll c[100010];
	int t[100010];
	int h[100010];
	int n;
	void add(int x,int y,ll a)
	{
		n++;
		v[n]=y;
		c[n]=a;
		t[n]=h[x];
		h[x]=n;
	}
	int d[100010];
	int e[100010];
	int op(int x)
	{
		return ((x-1)^1)+1;
	}
	int S,T;
	queue<int> q;
	int num;
	int cur[100010];
	void bfs()
	{
		memset(d,-1,sizeof d);
		d[T]=0;
		q.push(T);
		int x,i;
		while(!q.empty())
		{
			x=q.front();
			q.pop();
			e[d[x]]++;
			for(i=h[x];i;i=t[i])
				if(c[op(i)]&&d[v[i]]==-1)
				{
					d[v[i]]=d[x]+1;
					q.push(v[i]);
				}
		}
	}
	ll dfs(int x,ll flow)
	{
		if(x==T)
			return flow;
		ll s=0,u;
		for(int &i=cur[x];i;i=t[i])
			if(c[i]&&d[v[i]]==d[x]-1)
			{
				u=dfs(v[i],min(flow,c[i]));
				s+=u;
				flow-=u;
				c[i]-=u;
				c[op(i)]+=u;
				if(!flow)
					return s;
			}
		e[d[x]]--;
		if(!e[d[x]])
			d[S]=num;
		d[x]++;
		e[d[x]]++;
		cur[x]=h[x];
		return s;
	}
	ll solve()
	{
		ll ans=0;
		bfs();
		memcpy(cur,h,sizeof h);
		while(d[S]>=0&&d[S]<=num-1)
			ans+=dfs(S,inf);
		return ans;
	}
}
void add(int x,int y,int c)
{
	flow::add(x,y,c);
	flow::add(y,x,inf);
}
int f[110][110];
int lx[2510];
int ly[2510];
int lz[2510];
int n,m;
int main()
{
#ifndef ONLINE_JUDGE
	freopen("b.in","r",stdin);
	freopen("b.out","w",stdout);
#endif
	scanf("%d%d",&n,&m);
	int i,j,k;
	for(i=1;i<=m;i++)
	{
		scanf("%d%d%d",&lx[i],&ly[i],&lz[i]);
		lx[i]++;
		ly[i]++;
		f[lx[i]][ly[i]]=1;
	}
	for(k=1;k<=n;k++)
		for(i=1;i<=n;i++)
			if(i!=k&&f[i][k])
				for(j=1;j<=n;j++)
					if(j!=i&&j!=k)
						f[i][j]|=f[i][k]&&f[k][j];
	for(i=1;i<=n;i++)
		f[i][i]=1;
	flow::S=1;
	flow::T=n;
	flow::num=n;
	for(i=1;i<=m;i++)
		if(f[1][lx[i]]&&f[ly[i]][n])
			add(lx[i],ly[i],lz[i]);
	ll ans=flow::solve();
	if(ans>=inf)
		printf("-1\n");
	else
		printf("%lld\n",ans);
	return 0;
}