POJ1704 Georgia and Bob

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9771		Accepted: 3220

Description

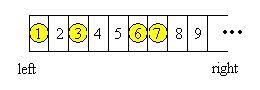
Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: 

Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

Given the initial positions of the n chessmen, can you predict who will finally win the game?

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

Output

For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

Sample Input

2
3
1 2 3
8
1 5 6 7 9 12 14 17

Sample Output

Bob will win
Georgia will win

Source

POJ Monthly--2004.07.18

博弈 脑洞题

操作时，棋子可以向前移动某范围内的任意距离←联想到nim问题←联想到sg函数

起初的想法是：将每个间隔长度看做nim游戏中的一堆石子长度，求所有间隔长度的异或和，若异或和为0，后手必胜。

果断WA掉

看到别人的解法是相邻棋子两两配对，每对之间的间隔当做nim石子。

似乎很有道理。如果每个间隔都算的话，减小一个间隔就会增加另一个间隔，而如果两两配对的话，假设a在b前面，a走x格，b也可以多走x格使得状态不变。

 /*by SilverN*/
 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<vector>
 using namespace std;
 const int mxn=;
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int T,n;
 int a[mxn],cnt=;
 int main(){
     int i,j,x;
     T=read();
     while(T--){
         n=read();
         int res=;
         a[]=;
         for(i=;i<=n;i++)a[i]=read();
         if(n&)a[++n]=;
         sort(a+,a+n+);
         for(i=;i<=n;i+=){
             res^=(a[i+]-a[i]-);
         }
         if(!res)printf("Bob will win\n");
         else printf("Georgia will win\n");
     }
     return ;
 }