Python基于皮尔逊系数实现股票预测
# -*- coding: utf-8 -*-
"""
Created on Mon Dec 2 14:49:59 2018 @author: zhen
""" import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from datetime import datetime def normal(a): #最大值最小值归一化
return (a - np.min(a)) / (np.max(a) - np.min(a)+0.000001) def normalization(x): # np.std:计算矩阵的标准差(方差的算术平方根)
return (x - np.mean(x)) / np.std(x) def corrcoef(a,b):
corrc = np.corrcoef(a,b) # 计算皮尔逊相关系数,用于度量两个变量之间的相关性,其值介于-1到1之间
corrc = corrc[0,1]
return (16 * ((1 - corrc) / (1 + corrc)) ** 1) # ** 表示乘方 startTimeStamp = datetime.now() # 获取当前时间
# 加载数据
filename = 'C:/Users/zhen/.spyder-py3/sh000300_2017.csv'
# 获取第一,二列的数据
all_date = pd.read_csv(filename,usecols=[0, 1, 3], dtype = 'str')
all_date = np.array(all_date)
data = all_date[:, 0]
times = all_date[:, 1] data_points = pd.read_csv(filename,usecols=[3])
data_points = np.array(data_points)
data_points = data_points[:,0] #数据 topk = 10 #只显示top-10
baselen = 100
basebegin = 361
basedata = data[basebegin]+' '+times[basebegin]+'~'+data[basebegin+baselen-1]+' '+times[basebegin+baselen-1]
base = data_points[basebegin:basebegin+baselen]#一天的数据是240个点
length = len(data_points) #数据长度 # 分割片段
subseries = []
dateseries = []
for j in range(0,length):
if (j < (basebegin - baselen) or j > (basebegin + baselen - 1)) and j <length - baselen:
subseries.append(data_points[j:j+baselen])
dateseries.append(j) #开始位置 # 片段搜索
listdistance = []
for i in range(0, len(subseries)):
tt = np.array(subseries[i])
distance = corrcoef(base, tt)
listdistance.append(distance) # 排序
index = np.argsort(listdistance,kind='quicksort') #排序,返回排序后的索引序列 # 显示,要匹配的数据
plt.figure(0)
plt.plot((base),label = basedata, linewidth='')
plt.legend(loc='upper left')
plt.title('Base data') # 原始数据
plt.figure(1)
num = index[0]
length = len(subseries[num])
begin = data[dateseries[num]]+' '+times[dateseries[num]]
end = data[dateseries[num]+length-1]+' '+times[dateseries[num]+length-1]
label = begin+'~'+end
plt.plot((subseries[num]), label=label, linewidth='')
plt.legend(loc='upper left')
plt.title('Similarity data') # 结果集对比
plt.figure(2)
plt.plot(normalization(base),label= basedata,linewidth='')
length = len(subseries[num])
begin = data[dateseries[num]] + ' ' + times[dateseries[num]]
end = data[dateseries[num] + length - 1] + ' ' + times[dateseries[num] + length - 1]
label = begin + '~' + end
plt.plot(normalization(subseries[num]), label=label, linewidth='')
plt.legend(loc='lower right')
plt.title('normal similarity search')
plt.show() endTimeStamp=datetime.now()
print('run time', (endTimeStamp-startTimeStamp).seconds, "s")
结果:
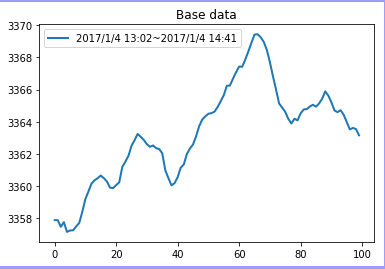


Python基于皮尔逊系数实现股票预测的更多相关文章
- 从欧几里得距离、向量、皮尔逊系数到http://guessthecorrelation.com/
一.欧几里得距离就是向量的距离公式 二.皮尔逊相关系数反应的就是线性相关 游戏http://guessthecorrelation.com/ 的秘诀也就是判断一组点的拟合线的斜率y/x ------- ...
- 皮尔逊相似度计算的例子(R语言)
编译最近的协同过滤算法皮尔逊相似度计算.下顺便研究R简单使用的语言.概率统计知识. 一.概率论和统计学概念复习 1)期望值(Expected Value) 由于这里每一个数都是等概率的.所以就当做是数 ...
- Pearson(皮尔逊)相关系数及MATLAB实现
转自:http://blog.csdn.net/wsywl/article/details/5727327 由于使用的统计相关系数比较频繁,所以这里就利用几篇文章简单介绍一下这些系数. 相关系数:考察 ...
- pandas通过皮尔逊积矩线性相关系数(Pearson's r)计算数据相关性
皮尔逊积矩线性相关系数(Pearson's r)用于计算两组数组之间是否有线性关联,举个例子: a = pd.Series([1,2,3,4,5,6,7,8,9,10]) b = pd.Series( ...
- Pearson(皮尔逊)相关系数
Pearson(皮尔逊)相关系数:也叫pearson积差相关系数.衡量两个连续变量之间的线性相关程度. 当两个变量都是正态连续变量,而且两者之间呈线性关系时,表现这两个变量之间相关程度用积差相关系数, ...
- 皮尔逊(Pearson)系数矩阵——numpy
一.原理 注意 专有名词.(例如:极高相关) 二.代码 import numpy as np f = open('../file/Pearson.csv', encoding='utf-8') dat ...
- np.corrcoef()方法计算数据皮尔逊积矩相关系数(Pearson's r)
上一篇通过公式自己写了一个计算两组数据的皮尔逊积矩相关系数(Pearson's r)的方法,但np已经提供了一个用于计算皮尔逊积矩相关系数(Pearson's r)的方法 np.corrcoef() ...
- 皮尔逊残差 | Pearson residual
参考:Pearson Residuals 这些概念到底是写什么?怎么产生的? 统计学功力太弱了!
- Spark Mllib里的如何对两组数据用皮尔逊计算相关系数
不多说,直接上干货! import org.apache.spark.mllib.stat.Statistics 具体,见 Spark Mllib机器学习实战的第4章 Mllib基本数据类型和Mlli ...
随机推荐
- ASP.NET Core身份认证服务框架IdentityServer4(2)-整体介绍
一.整体情况 现代应用程序看起来更像这个: 最常见的相互作用: 浏览器与Web应用程序的通信 Browser -> Web App Web应用程序与Web API通信 基于浏览器的应用程序与We ...
- Android切换横竖屏不销毁前台Activity,也不影响后台Activity
在切换屏幕方向的时候,Activity默认会走销毁->重建的生命周期,而有时候我们不希望如此,就需要做些额外的设置了: 1.在AndroidMainifest.xml中对应的Activity标签 ...
- java发送http get请求的两种方式
长话短说,废话不说 一.第一种方式,通过HttpClient方式,代码如下: public static String httpGet(String url, String charset) thro ...
- python 加密算法及其相关模块的学习(hashlib,random,string,math)
加密算法介绍 一,HASH Hash,一般翻译做“散列”,也有直接音译为”哈希”的,就是把任意长度的输入(又叫做预映射,pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值.这种 ...
- SpringBoot快速引入第三方jar包
工作中,我们常会用到第三方jar包,而这些jar包往往在maven仓库是搜不到的,下面推荐一种简单.快速的引入第三方依赖的方法: 比如第三方jar包在lib文件夹下,对pom.xml的配置如下: &l ...
- 十大经典排序算法详细总结(含JAVA代码实现)
原文出处:http://www.cnblogs.com/guoyaohua/p/8600214.html 0.排序算法说明 0.1 排序的定义 对一序列对象根据某个关键字进行排序. 0.2 术语说明 ...
- TCP三次握手与Tcpdump抓包分析过程
一.TCP连接建立(三次握手) 过程 客户端A,服务器B,初始序号seq,确认号ack 初始状态:B处于监听状态,A处于打开状态 A -> B : seq = x (A向B发送连接请求报文段,A ...
- NPOI导出EXCEL报_服务器无法在发送 HTTP 标头之后追加标头
虽然发表了2篇关于NPOI导出EXCEL的文章,但是最近再次使用的时候,把以前的代码粘贴过来,居然报了一个错误: “服务器无法在发送 HTTP 标头之后追加标头” 后来也查询了很多其他同学的文章,都没 ...
- [转]Angular4首页加载慢优化之路
本文转自:https://blog.csdn.net/itest_2016/article/details/80048398 Angular是一个比较完善的前端MVC框架,包含了模板,数据双向绑定,路 ...
- SQL 常用的判断、连表、跨库、去重、分组、ROW_NUMBER()分析函数SQL用法
常用的SQL 由浅入深 大致上回想一下自己常用的SQL,并做个记录,目标是实现可以通过在此页面查找到自己需要的SQL ,陆续补充 有不足之处,请提醒改正 首先我创建了两个库,每个库两张表.(工作 ...
