【数学基础篇】---详解极限与微分学与Jensen 不等式
一、前述
数学基础知识对机器学习还有深度学习的知识点理解尤为重要,本节主要讲解极限等相关知识。
二、极限
1、例子
当 x 趋于 0 的时候,sin(x) 与 tan(x) 都趋于 0. 但是哪一个趋于 0 的速度更快一些呢?
我们考察这两个函数的商的极限,
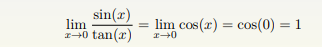
所以当 x → 0 的时候,sin(x) 与 tan(x) 是同样级别的无穷小。
2、相关定理
如果三个函数满足 f(x) ≤ g(x) ≤ h(x), 而且他们都在 x0 处有极 限,那么
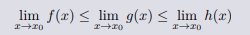
重要极限:

三、微分学
微分学的核心思想: 逼近.
1、函数导数:
如果一个函数 f(x) 在 x0 附近有定义,而且存在极限。
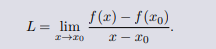
那么 f(x) 在 x0 处可导且导数 f ′ (x0) = L.
无穷小量表述: 线性逼近。
Definition (函数的高阶导数)
如果函数的导数函数仍然可导,那么导数函数的导数是二阶导 数,二阶导数函数的导数是三阶导数. 一般地记为
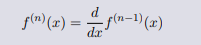
或者进一步
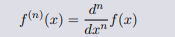
导数是对函数进行线性逼近,高阶导数是对导数函数的进一步逼 近,因为没有更好的办法,所以数学家选择继续使用线性逼近.
Example (初等函数的导数)
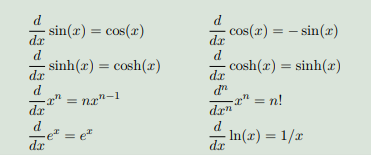
2、微分学:多元函数

且 Lx, Ly 分别是 f 在 x, y 方向上的偏导数. 一般记为
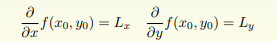
3、Definition (高阶偏导数)

并且二阶偏导数为
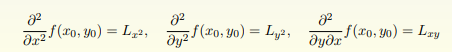
4、Example (偏导数的例子)
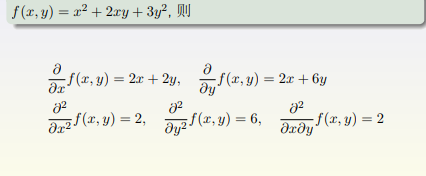
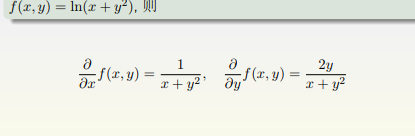

5、求导法则
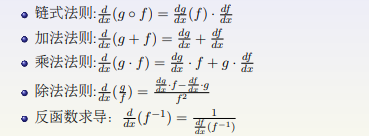
6.总结
微分学的核心思想是逼近. 一阶导数:线性逼近 二阶导数:二次逼近 导数计算:求导法则
四、泰勒级数
1、泰勒/迈克劳林级数: 多项式逼近。

2、泰勒级数: 例子
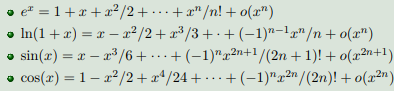
3、应用
泰勒级数是一元微分逼近的顶峰,所以有关于一元微分逼近的问 题请尽情使用.
罗比塔法则
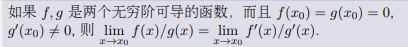
证明:
因为是在 x0 附近的极限问题,我们使用泰勒级数来思考这个问题
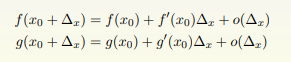
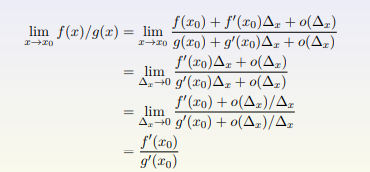
4、小结 (泰勒级数)
泰勒级数本质是多项式逼近
特殊函数的泰勒级数可以适当记一下
泰勒级数可以应用于很多与逼近相关的问题。
五、牛顿法与梯度下降法
很多机器学习或者统计的算法最后都转化成一个优化的问题. 也 就是求某一个损失函数的极小值的问题, 在本课范围内我们考虑 可微分的函数极小值问题.
1、优化问题
对于一个无穷可微的函数 f(x),如何寻找他的极小值点.
极值点条件。
全局极小值: 如果对于任何 x˜, 都有 f(x∗) ≤ f(˜x),那么 x∗ 就是全局极小值点.
局部极小值: 如果存在一个正数 δ 使得,对于任何满足 |x˜ − x∗| < δ 的 x˜, 都有 f(x∗) ≤ f(˜x),那么 x∗ 就是局部极 小值点.(方圆 δ 内的极小值点)
不论是全局极小值还是局部极小值一定满足一阶导数/梯度 为零,f ′ = 0 或者 ∇f = 0.
2、局部极值算法
这两种方法都只能寻找局部极值 这两种方法都要求必须给出一个初始点 x0
数学原理:牛顿法使用二阶逼近(等价于使用二阶泰勒级数),梯度下降法使用一阶逼近
牛顿法对局部凸的函数找到极小值,对局部凹的函数找到极 大值,对局部不凸不凹的可能会找到鞍点.
梯度下降法一般不会找到最大值,但是同样可能会找到鞍 点.
当初始值选取合理的情况下,牛顿法比梯度下降法收敛速度 快.
牛顿法要求估计二阶导数,计算难度更大.
3、牛顿法
首先在初始点 x0 处,写出二阶泰勒级数。
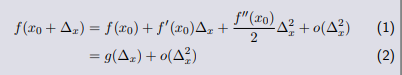

多变量函数二阶逼近


4、梯度下降法:多变量函数一阶逼近
如果函数 f(x) 是个多元函数,x 是一个向量. 在 x0 处对f做线性逼近。

5、小结 (牛顿法与梯度下降法)
牛顿法与梯度下降法本质上都是对目标函数进行局部逼近.
因为是局部逼近所以也只能寻找局部极值
牛顿法收敛步骤比较少,但是梯度下降法每一步计算更加简单,牛顿法不仅给出梯度的方向还给出具体应该走多少。梯度法的r只能自己定义。
不同的算法之间很难说哪一个更好,选择算法还要具体问题 具体分析(这也是数据科学家存在的意义之一)
梯度本身是向着最大方向的,加个负号才是向着最小方向的。
六、凸函数与琴生不等式
1、Definition (凸函数)
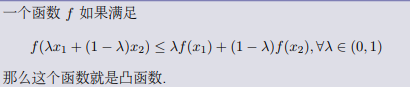
把如上定义中的 ≤ 换成 <, 那么这个函数就叫做严格凸函数。
2、(凸函数判断准则)

如果 f 是多元函数,x 是个向量, 那么 f 是凸函数的条件变为Hf 是一个半正定矩阵。
3、凸函数重要性质: 琴生不等式)
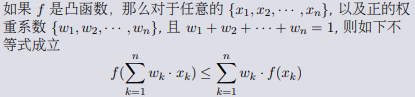
【数学基础篇】---详解极限与微分学与Jensen 不等式的更多相关文章
- PHP函数篇详解十进制、二进制、八进制和十六进制转换函数说明
PHP函数篇详解十进制.二进制.八进制和十六进制转换函数说明 作者: 字体:[增加 减小] 类型:转载 中文字符编码研究系列第一期,PHP函数篇详解十进制.二进制.八进制和十六进制互相转换函数说明 ...
- 走向DBA[MSSQL篇] 详解游标
原文:走向DBA[MSSQL篇] 详解游标 前篇回顾:上一篇虫子介绍了一些不常用的数据过滤方式,本篇详细介绍下游标. 概念 简单点说游标的作用就是存储一个结果集,并根据语法将这个结果集的数据逐条处理. ...
- Scala进阶之路-Scala函数篇详解
Scala进阶之路-Scala函数篇详解 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 一.传值调用和传名调用 /* @author :yinzhengjie Blog:http: ...
- CentOS 7 下编译安装lnmp之PHP篇详解
一.安装环境 宿主机=> win7,虚拟机 centos => 系统版本:centos-release-7-5.1804.el7.centos.x86_64 二.PHP下载 官网 http ...
- CentOS 7 下编译安装lnmp之MySQL篇详解
一.安装环境 宿主机=> win7,虚拟机 centos => 系统版本:centos-release-7-5.1804.el7.centos.x86_64 二.MySQL下载 MySQL ...
- CentOS 7 下编译安装lnmp之nginx篇详解
一.安装环境 宿主机=> win7,虚拟机 centos => 系统版本:CentOS Linux release 7.5.1804 (Core),ip地址 192.168.1.168 ...
- Canal:同步mysql增量数据工具,一篇详解核心知识点
老刘是一名即将找工作的研二学生,写博客一方面是总结大数据开发的知识点,一方面是希望能够帮助伙伴让自学从此不求人.由于老刘是自学大数据开发,博客中肯定会存在一些不足,还希望大家能够批评指正,让我们一起进 ...
- java提高篇-----详解java的四舍五入与保留位
转载:http://blog.csdn.net/chenssy/article/details/12719811 四舍五入是我们小学的数学问题,这个问题对于我们程序猿来说就类似于1到10的加减乘除那么 ...
- 组件--Fragment(碎片)第二篇详解
感觉之前看的还是不清楚,重新再研究了一次 Fragment常用的三个类: android.app.Fragment 主要用于定义Fragment android.app.FragmentManager ...
随机推荐
- Python HTTP库requests中文页面乱码解决方案!
http://www.cnblogs.com/bitpeng/p/4748872.html Python中文乱码,是一个很大的坑,自己不知道在这里遇到多少问题了.还好通过自己不断的总结,现在遇到乱码的 ...
- sudo pip install MySQLdb
安装数据库第三方包,报错: Could not find a version that satisfies the requirement MySQLdb (from versions: )No ma ...
- sql语句联表更新(从一个数据库中的一张表更新到另一个数据库的另一张表)
一.sql server数据库写法: update a set a.ksgmm=b.ksgmm,a.ksgm=b.ksgm,a.scztm=b.scztm,a.sczt=b.sczt from lan ...
- HiJson(Json格式化工具)64位中文版下载 v2.1.2
链接:https://pan.baidu.com/s/15gMvig15iUjpqSX7nUZ-5Q 密码:8086
- PHP后端之验证码
PHP后端之验证码 前言: 打算写一些实际开发中遇到的东西.我这个人记性不好,觉得记下来,以后就算想找,也能找得到. PHP,可能很长一段时间都不会使用了.所以还是留一些记录. 另外还有一些服务器架设 ...
- Unity3D学习(二):使用JSON进行对象数据的存储读取
前言 前段时间完成了自己的小游戏Konster的制作,今天重新又看了下代码.原先对关卡解锁数据的存储时用了Unity自带的PlayerPref(字典式存储数据). 读取关卡数据的代码: void Aw ...
- 关于Java的散列桶, 以及附上一个案例-重写map集合
为速度而散列: SlowMap.java说明了创建一个新的Map并不困难.但正如它的名称SlowMap所示,它不会很快,如果有更好的选择就应该放弃它.它的问题在于对键的查询,键没有按照任何特定的顺序保 ...
- Struts标签库详解【1】
struts2标签详解 要在jsp中使用Struts2的标志,先要指明标志的引入.通过jsp的代码的顶部加入以下的代码: <%@taglib prefix="s" uri=& ...
- 【转】tomcat logs 目录下各日志文件的含义
tomcat每次启动时,自动在logs目录下生产以下日志文件,按照日期自动备份 localhost.2016-07-05.txt //经常用到的文件之一 ,程序异常没有被捕获的时候抛出的地方 ...
- Windows 安装 Vue
引言 在公司 linux 环境下安装不顺利,回家在 windows 下操作感觉到一种幸福 nginx 先安装了 nginx,其实跟 vue 没关系,只是打算用它做 web 服务,此处略过 nginx ...
