PKU 1129 Channel Allocation(染色问题||搜索+剪枝)

题目大意建模：

一个有N个节点的无向图，要求对每个节点进行染色，使得相邻两个节点颜色都不同，问最少需要多少种颜色？

那么题目就变成了一个经典的图的染色问题

例如:N=7

A:BCDEFG

B:ACDEFG

C:ABD

D:ABCE

E:ABDF

F:ABEG

G:ABF

画成图就是：

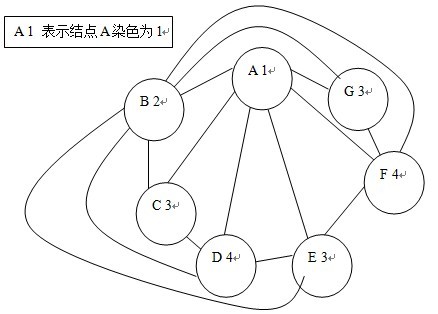
首先考虑四色定理:任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色

judge(int x,int y)枚举判断x的邻接点中是否着色y颜色的

1.正向考虑dfs(int num,int color)从第一个点开始从前往后用color种颜色给num个点着色

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
char ch[];
bool vis[];
int n,col[],graph[][];
bool judge(int x,int y)
{//判断在x点是否可以着色y
    for(int i=;i<n;i++){
        if(graph[x][i])
            if(col[i]==y) return false;
    }
    return true;
}
bool dfs(int num,int color)
{
    if(num>n)
        return true;
    for(int i=;i<num;i++){//dfs()函数含义体现在此处for循环
        if(!vis[i]){
            vis[i]=true;
            for(int j=;j<=color;j++){
                if(judge(i,j)){
                    col[i]=j;//着色
                    if(dfs(num+,color))
                        return true;
                }
            }
            vis[i]=false;
        }
    }
    return false;
}
int main()
{
    while(scanf("%d",&n),n){
        memset(graph,,sizeof(graph));
        for(int i=;i<n;i++){
            cin>>ch;for(int j=;j<strlen(ch);j++)
                graph[ch[]-'A'][ch[j]-'A']=;
        }
        for(int i=;i<=;i++){
            memset(vis,,sizeof(vis));
            if(dfs(,i)){
                if(i==)
                    printf("1 channel needed.\n");
                else
                    printf("%d channels needed.\n",i);
                break;
            }
        }
    }
}

2.反向考虑dfs(int num,int color)从第n个点开始从后往前用color种颜色给剩下的num个点着色,同时减少vis[30]数组的开辟

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
char ch[];
int n,col[],graph[][];
bool judge(int x,int y)
{
    for(int i=;i<n;i++){
        if(graph[x][i])
            if(col[i]==y) return false;
    }
    return true;
}
bool dfs(int num,int color)
{
    if(!num)
        return true;//dfs()函数含义体现在此处for循环
    for(int i=num-;i>=;i--){//或者for(int i=0;i<num;i++)
        if(!col[i]){
            for(int j=;j<=color;j++){
                if(judge(i,j)){
                    col[i]=j;
                    if(dfs(num-,color))
                        return true;
                }
            }
            col[i]=;
        }
    }
    return false;
}
int main()
{
    while(scanf("%d",&n),n){
        memset(graph,,sizeof(graph));
        for(int i=;i<n;i++){
            cin>>ch;for(int j=;j<strlen(ch);j++)
                graph[ch[]-'A'][ch[j]-'A']=;
        }
        for(int i=;i<=;i++){
            memset(col,,sizeof(col));
            if(dfs(n,i)){
                if(i==)
                    printf("1 channel needed.\n");
                else
                    printf("%d channels needed.\n",i);
                break;
            }
        }
    }
}

3.dfs(int num,int color)从第num个点开始用color种颜色着色,函数含义体现在自身

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
char ch[];
bool vis[];
int n,col[],graph[][];
bool judge(int x,int y)
{
    for(int i=;i<n;i++){
        if(graph[x][i])
            if(col[i]==y) return false;
    }
    return true;
}
bool dfs(int num,int color)
{
    if(num>n)
        return true;
    for(int i=num-;i<n;i++){//和第一种正向考虑的区别
        if(!vis[i]){
            vis[i]=;
            for(int j=;j<=color;j++){
                if(judge(i,j)){
                    col[i]=j;
                    if(dfs(num+,color))
                        return true;
                }
            }
            vis[i]=;
        }
    }
    return false;
}
int main()
{
    while(scanf("%d",&n),n){
        memset(graph,,sizeof(graph));
        for(int i=;i<n;i++){
            cin>>ch;for(int j=;j<strlen(ch);j++)
                graph[ch[]-'A'][ch[j]-'A']=;
        }
        for(int i=;i<=;i++){
            memset(vis,,sizeof(vis));
            if(dfs(,i)){
                if(i==)
                    printf("1 channel needed.\n");
                else
                    printf("%d channels needed.\n",i);
                break;
            }
        }
    }
}

暴力搜索

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
bool graph[][];
char ch[];
int col[],colornum;
int n,mincolor;
bool judge(int x,int y)
{
    for(int i=;i<n;i++){
        if(graph[x][i])
            if(col[i]==y) return false;
    }
    return true;
}
bool flag;
void dfs(int i)
{
    if(flag) return;
    if(i==n){//剪枝
        mincolor=colornum;
        flag=;
    }//判断用过的颜色里是否有可用的
    for(int j=;j<=colornum;j++){
        if(judge(i,j)){
            col[i]=j;
            dfs(i+);
            col[i]=;//还原到dfs(i+1)之前的状态,因为可能还可以染其他颜色
        }
    }
    colornum++;//上面颜色都不行的话再选用一种新的颜色
    col[i]=colornum;
    dfs(i+);
    col[i]=;//还原到dfs(i+1)之前的状态
    colornum--;//还原,因为i都没被染色,所以新加的颜色肯定要退回去
}
int main()
{
    while(scanf("%d",&n),n){
        memset(graph,,sizeof(graph));
        for(int i=;i<n;i++){
            cin>>ch;
            for(int j=;j<strlen(ch);j++)
                graph[ch[]-'A'][ch[j]-'A']=;
        }
        flag=,colornum=;
        memset(col,,sizeof(col));
        dfs();//注意 不是dfs(1),因为第一个点的编号为0
        if(mincolor==)
            printf("1 channel needed.\n");
        else
            printf("%d channels needed.\n",mincolor);
    }
}