[bzoj1016][JSOI2008]最小生成树计数 (Kruskal + Matrix Tree 定理)

Description

现在给出了一个简单无向加权图。你不满足于求出这个图的最小生成树，而希望知道这个图中有多少个不同的最小生成树。（如果两颗最小生成树中至少有一条边不同，则这两个最小生成树就是不同的）。由于不同的最小生成树可能很多，所以你只需要输出方案数对31011的模就可以了。

Input

第一行包含两个数，n和m，其中1<=n<=100; 1<=m<=1000; 表示该无向图的节点数和边数。每个节点用1~n的整数编号。接下来的m行，每行包含两个整数：a, b, c，表示节点a, b之间的边的权值为c，其中1<=c<=1,000,000,000。数据保证不会出现自回边和重边。注意：具有相同权值的边不会超过10 条。

Output

输出不同的最小生成树有多少个。你只需要输出数量对31011的模就可以了。

Sample Input

4 6
1 2 1
1 3 1
1 4 1
2 3 2
2 4 1
3 4 1

Sample Output

分析

先回忆一下求解最小生成树的过程：将边排序，贪心添加进当前生成森林中。由Kruskal算法的性质:【传送门】，在算法开始处理权值为val的边前，原图会形成若干个连通块，如图所示：

图中的虚线表示原图中所有权值为val的边。通过与Kruskal算法相似的证明，我们可以知道在处理完边数为val的边后，形成的连通分量是一定的。也就是说，在这一过程中不论我们采取怎样的顺序，图中的点集S1,S2,S3一定连通，且这个新的连通块恰好是新的点集的一个最小生成树。

那么，我们如何计算出这一过程可以有多少种连接方式呢？我们先把三个连通块都缩成点：

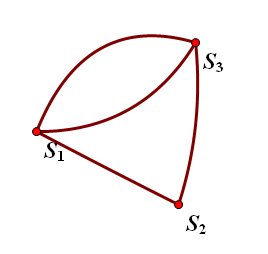
我们的问题就变成了：在图中选取若干条边使得S1,S2,S3构成一棵树有多少种方案？这就转化为了一个数学问题：一般生成树计数，可以用Matrix-Tree定理来计算。

于是我们就得到了本题的解法：1、将所有边升序排列；2、循环处理每一种权值形成的集合；3、对于同一种权值，利用Matrix-Tree定理求出当前处理的所有边可以产生的那些连通块的连接方式总数，乘入答案；4、将当前边可以产生的连通块缩成点。具体实现细节请看代码中的注释：

;
, c = getchar();
+ c - , maxm = , mod = ;
, *Mat[], sum;
;i <= x;++i)pre[i] = i;}
;i < M;++i)
;i < ;++i)
];;
;i < n;++i){
;j < n;++j){
], block[], cnt;
;
,j = ;i < len;++i){
] = tmp[];
;i < j;++i)
])block[cnt++] = tmp[i];     ;i < cnt;++i);j < cnt;++j)
         Mat[i][j] = ;

     tmpS.init(cnt);

     ;i < len;++i){
                            A[i].u = index(A[i].u);
         A[i].v = index(A[i].v);          ++Mat[A[i].v][A[i].v];
                    --Mat[A[i].v][A[i].u];
         tmpS.link(A[i].u, A[i].v);
     }
           ;i < cnt;++i)
         ))){
             ++Mat[a][a], ++Mat[b][b];
                           tmpS.link(a, b);
         }

     Ans = Ans * det(cnt) % mod;
}
inline      , j = , t;
               )calc(E + i, j - i);
                   i = j++;
     }
     )printf(          printf( }
           freopen(          #ifndef ONLINE_JUDGE
     freopen(     freopen(               init();
     work();

     ;
}

Kruskal + Matrix Tree定理