codeforce D. White Lines

二维前缀和

给你一个n*n的矩阵，里面有两种字符，‘W’和‘B’，代表black 和white 。其实这个矩阵就是一个方形画板，你有一个k*k的橡皮只能用一次，使k*k的矩阵里的B变成W，问完全空白的行和列的总数？

思路：

用1代替B，0代替W，然后维护一个前缀和数组，看能否用一个橡皮的操作使这一列或行的前缀和变为0，然后维护答案就好了，具体操作可以把列对称成行，相当于搞两个不同的数组，这样就只需要搞两个数组的行就可以了。如图：

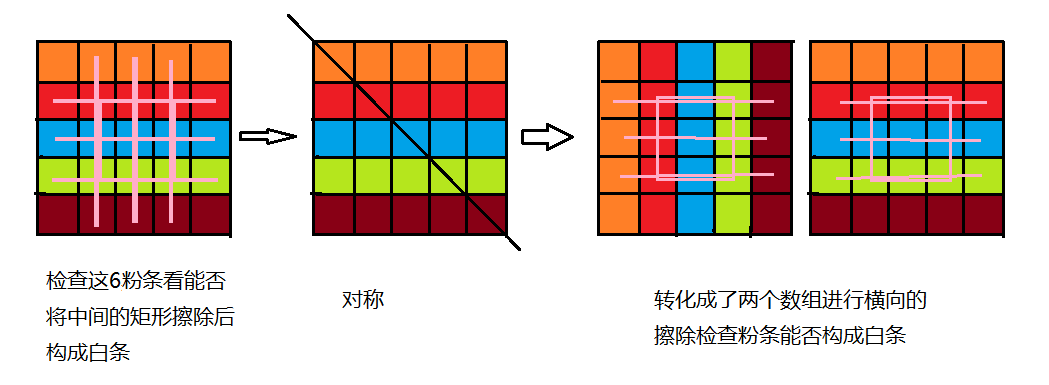
剩下的具体思路看代码吧

 #include<bits/stdc++.h>
 using namespace std;
 const int N=;
 int n,k,ans,tot,r[N][N],c[N][N],okr[N][N],okc[N][N];
 char mp[N][N];
 int main()
 {
     scanf("%d%d%*c",&n,&k);
     for(int i=;i<=n;scanf("%*c"),i++)
         for(int j=;j<=n;j++)
             scanf("%c",&mp[i][j]);
 //  输入
     for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
             r[i][j]=r[i][j-]+(mp[i][j]=='B'),c[i][j]=c[i][j-]+(mp[j][i]=='B');
 //  记录 1代表'B'，0代表'W';
 //  这里将数组关于斜对角线对称一下，问题就变成了统计对称前擦除操作后有多少个全0的行！
 //  和对称后的那个数组擦除操作后有多少的全0的行（因为对称后列变成了行）如上图
     for(int i=;i<=n;i++)tot+=(r[i][n]==)+(c[i][n]==);
 // tot是没有擦除操作就是全0行的个数
     for(int i=;i<=n;i++)
         for(int j=;j<=n-k+;j++)
             okr[i][j]=(r[i][j+k-]-r[i][j-]==r[i][n]&&r[i][n]!=)+okr[i-][j],
             //这一行中只有长度为k的区间有1等价于【(r[i][j+k-1]-r[i][j-1]==r[i][n]】
             // 【r[i][n]!=0】避免重复计算初始为全0行的个数
             //那么可以通过擦除操作对答案做出贡献 ，并作一个前缀和
             okc[i][j]=(c[i][j+k-]-c[i][j-]==c[i][n]&&c[i][n]!=)+okc[i-][j];
             //同理
     for(int i=;i<=n-k+;i++)
         for(int j=;j<=n-k+;j++)
             ans=max(ans,tot+okr[i+k-][j]-okr[i-][j]+okc[j+k-][i]-okc[j-][i]);
             //维护一个初始全0行+操作后对答案贡献的两个区间和
     printf("%d",ans);
 }