POJ 1066 - Treasure Hunt - [枚举+判断线段相交]

题目链接：http://poj.org/problem?id=1066

Time Limit: 1000MS Memory Limit: 10000K

Description

Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors. 
An example is shown below: 

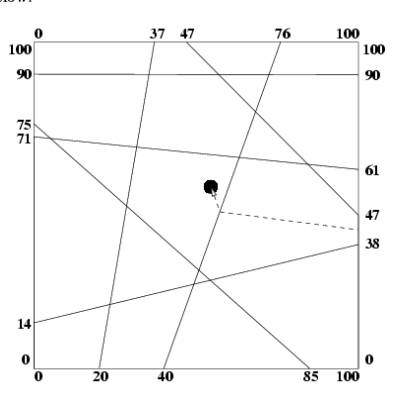
Input

The input will consist of one case. The first line will be an integer n (0 <= n <= 30) specifying number of interior walls, followed by n lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4 enclosing walls of the pyramid have fixed endpoints at (0,0); (0,100); (100,100) and (100,0) and are not included in the list of walls. The interior walls always span from one exterior wall to another exterior wall and are arranged such that no more than two walls intersect at any point. You may assume that no two given walls coincide. After the listing of the interior walls there will be one final line containing the floating point coordinates of the treasure in the treasure room (guaranteed not to lie on a wall).

Output

Print a single line listing the minimum number of doors which need to be created, in the format shown below.

Sample Input

7
20 0 37 100
40 0 76 100
85 0 0 75
100 90 0 90
0 71 100 61
0 14 100 38
100 47 47 100
54.5 55.4 

Sample Output

Number of doors = 2

题意：

一个正方形底的金字塔，坐标为(0,0)->(100,100)，里面情况类似于上图，有许多直接连接在最外层正方形上的墙，把整个金字塔底部分割成许多小房间；

现在专家们已经确定，其中某一个房间为宝藏房，并且得到了一个位于该房间内的点坐标，记为点p；

现在专家们要从最外面进行爆破开门法，一直炸到宝藏房，求最少需要开多少扇门。

题解：

枚举(0,0)-(0,100)-(100,100)-(100,0)这个正方形上的所有点（其实就是所有墙的端点），记为点q；

连接p与q两点得到一条线段，再去枚举所有的墙，通过判断是否规范相交确定一路上要经过多少堵墙，记为cnt；

顺便把(0,0)、(0,100)、(100,100)、(100,0)这四个点也按上面的办法去算一下cnt；

取所有cnt中最小的，加上1（外墙上还要开扇门），即为答案；

AC代码：

#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
 
const double eps = 1e-;
 
struct Point{
    double x,y;
    Point(double tx=,double ty=):x(tx),y(ty){}
};
typedef Point Vctor;
 
//向量的加减乘除
Vctor operator + (Vctor A,Vctor B){return Vctor(A.x+B.x,A.y+B.y);}
Vctor operator - (Point A,Point B){return Vctor(A.x-B.x,A.y-B.y);}
Vctor operator * (Vctor A,double p){return Vctor(A.x*p,A.y*p);}
Vctor operator / (Vctor A,double p){return Vctor(A.x/p,A.y/p);}
 
int dcmp(double x)
{
    if(fabs(x)<eps) return ;
    else return (x<)?(-):();
}
bool operator == (Point A,Point B){return dcmp(A.x-B.x)== && dcmp(A.y-B.y)==;}
 
double Cross(Vctor A,Vctor B){return A.x*B.y-A.y*B.x;}
 
//判断线段是否规范相交
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)
{
    double c1 = Cross(a2 - a1,b1 - a1), c2 = Cross(a2 - a1,b2 - a1),
           c3 = Cross(b2 - b1,a1 - b1), c4 = Cross(b2 - b1,a2 - b1);
    return dcmp(c1)*dcmp(c2)< && dcmp(c3)*dcmp(c4)<;
}
 
int n;
struct Seg{
    Point a,b;
}wall[];
Point p;
int test(const Point& q)
{
    int cnt=;
    for(int i=;i<=n;i++)
        if(SegmentProperIntersection(p,q,wall[i].a,wall[i].b)) cnt++;
    return cnt;
}
int main()
{
    cin>>n;
    for(int i=;i<=n;i++) scanf("%lf%lf%lf%lf",&wall[i].a.x,&wall[i].a.y,&wall[i].b.x,&wall[i].b.y);
    cin>>p.x>>p.y;
 
    int ans=0x3f3f3f3f;
    for(int i=,tmp;i<=n;i++)
    {
        ans=min(test(wall[i].a),ans);
        ans=min(test(wall[i].b),ans);
    }
    ans=min(test(Point(,)),ans);
    ans=min(test(Point(,)),ans);
    ans=min(test(Point(,)),ans);
    ans=min(test(Point(,)),ans);
 
    cout<<"Number of doors = "<<ans+<<endl;
}