【树形DP】【P1364】医院放置

传送门

Description

　　

　　设有一棵二叉树，如图：

　　　

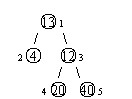
　　其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为1。如上图中，

　　若医院建在1 处，则距离和=4+12+2*20+2*40=136；若医院建在3 处，则距离和=4*2+13+20+40=81……

Input　　

　　第一行一个整数n，表示树的结点数。

　　接下来的n行每行描述了一个结点的状况，包含三个整数，整数之间用空格(一个或多个)分隔，其中：第一个数为居民人口数；第二个数为左链接，为0表示无链接；第三个数为右链接。

Output

　　一个整数，表示最小距离和。

Sample Input

Sample Output

Hint

　　n≤100

Solution

　　事实上这是一道非常简单的全员最短路，直接floyd就能够AC，但是冲着DP的标签，有一种树形DP的方法，在常规的树形DP中，由儿子更新父亲的信息，但在本题中，需要预处理根节点的信息，然后通过父亲更新儿子。复杂度O(n)。

　　记f[i]为在i点放医院的答案，sz[i]为以i为根的子树的节点权值和，手动画图可推知，f[son]=f[fa]+(sz[1]-sz[to])-sz[to]=f[fa]+sz[1]-2*sz[to]。预处理f[1]，dfs更新子树即可

Code

#include<cstdio>
#define maxn 105

inline void qr(int &x) {
    char ch=getchar();int f=;
    while(ch>''||ch<'')    {
        if(ch=='-')    f=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='')    x=(x<<)+(x<<)+(ch^),ch=getchar();
    x*=f;
}

inline int max(int a,int b) {return a>b?a:b;}
inline int min(int a,int b) {return a<b?a:b;}
inline int abs(int x) {return x<?-x:x;}

inline void swap(int &a,int &b) {
    int c=a;a=b;b=c;
}

struct Edge {
    int to,nxt;
};
Edge edge[maxn];int hd[maxn],ecnt;
inline void cont(int from,int to) {
    edge[++ecnt].to=to;
    edge[ecnt].nxt=hd[from];
    hd[from]=ecnt;
}

int n,num[maxn],a,sz[maxn],frog[maxn],deepth[maxn],ans;

void dfs(int fa,int k) {
    deepth[k]=deepth[fa]+;sz[k]=num[k];
    if(!hd[k])     return;
    for(int i=hd[k];i;i=edge[i].nxt) {
        dfs(k,edge[i].to);
        sz[k]+=sz[edge[i].to];
    }
}

void search(int k) {
    for(int i=hd[k];i;i=edge[i].nxt) {
        int &to=edge[i].to;
        frog[to]=frog[k]+sz[]-*sz[to];
        search(to);
    }
    ans=min(ans,frog[k]);
}

int main() {
    qr(n);
    for(int i=;i<=n;++i) {
        qr(num[i]);
        a=;qr(a);
        if(a)    cont(i,a);
        a=;qr(a);
        if(a)    cont(i,a);
    }
    deepth[]=-;
    dfs(,);
    for(int i=;i<=n;++i) frog[]+=num[i]*deepth[i];
    ans=frog[];
    search();
    printf("%d\n",ans);
    return ;
}

Summary

　　1、对于一般的树形DP，其状态设计一般为“以i为根的子树……”，通过儿子更新父亲。但是有一些特殊的DP形式，需要通过父亲更新儿子，f[i]表示“在i点……”。

　　2、对于树上的题，可以优先思考图论问题，然后再思考DP，有些题使用图论可以轻松解决。