poj 1654：Area 区域 ---- 叉积（求多边形面积）

Area

 

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 19398		Accepted: 5311

利用叉积求多边形面积，可以分解成多个三角形

利用面积公式，S=1/2*abs((x0*y1-x1*y0)+(x1*y2-x2*y1)...+(xn*yn-1-xn-1*yn)+(xn*y0-x0*yn)) ,把相邻两点和原点组成一个三角形，而总面积是这n个三角形面积的和，而三角形面积是两个相邻边向量的叉积

Description

You are going to compute the area of a special kind of polygon. One vertex of the polygon is the origin of the orthogonal coordinate system. From this vertex, you may go step by step to the following vertexes of the polygon until back to the initial vertex. For each step you may go North, West, South or East with step length of 1 unit, or go Northwest, Northeast, Southwest or Southeast with step length of square root of 2. 

你要计算一种特殊的多边形的面积。一个顶点的多边形是正交坐标系的原点。从这个顶点,你可以走了一步一步的多边形的顶点后,直到回到最初的顶点。为每个步骤你可以去北、西、南、东与步长为1单位,或去西北,东北,西南或东南√2步长。

For example, this is a legal polygon to be computed and its area is 2.5: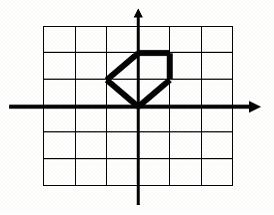 

Input

The first line of input is an integer t (1 <= t <= 20), the number of the test polygons. Each of the following lines contains a string composed of digits 1-9 describing how the polygon is formed by walking from the origin. Here 8, 2, 6 and 4 represent North, South, East and West, while 9, 7, 3 and 1 denote Northeast, Northwest, Southeast and Southwest respectively. Number 5 only appears at the end of the sequence indicating the stop of walking. You may assume that the input polygon is valid which means that the endpoint is always the start point and the sides of the polygon are not cross to each other.Each line may contain up to 1000000 digits.

Output

For each polygon, print its area on a single line.

Sample Input

4
5
825
6725
6244865

Sample Output

0
0
0.5
2

#include<cstdio>
#define ll long long
ll n,m,t,x1,x2,y1,y2,ans;
int dx[10]={0,1,1,1,0,0,0,-1,-1,-1};
int dy[10]={0,-1,0,1,-1,0,1,-1,0,1};
ll abs(ll a){return a<0?-a:a;}
int main()
{
	scanf("%d",&t);
	for(int i=0;i<t;i++)
	{
		x2=y2=ans=0;
		char p=getchar();
		while(p=getchar())
		{
			ll tmp=p-'0';
			if(tmp==5) break;
			x1=x2,y1=y2;
			x2+=dx[tmp],y2+=dy[tmp];
			ans+=(x1*y2-x2*y1);
		}
		ans=abs(ans);
		if(ans%2==0) printf("%lld\n",ans/2);
		else printf("%lld.5\n",ans/2);
	}
}