关于verilog中的signed类型

在数字电路中，出于应用的需要，我们可以使用无符号数，即包括0及整数的集合；也可以使用有符号数，即包括0和正负数的集合。在更加复杂的系统中，也许这两种类型的数，我们都会用到。

有符号数通常以2的补码形式来表示。图1列出了4位二进制表示法所对应正负数。进一步观察，我们发现两种类型数的加减法是一样的，做加法和减法就是 在数轮上按正时钟转转或按反时钟转。比方说，1001+0100，意味着从1001按照顺时钟方向移动4个位置，其结果为1101。在无符号数类型中，它 代表（+9）+（+4）=+13；而在有符号数类型中，它则代表（-7）+（+4）=-3。从数轮上看，若是加法所得的结果溢出了，那么也就是穿越了数轮 的临界点。注意这个临界点对于无符号数和有符号数来说，是不一样的：无符号数，是介于1111和0000之间；有符号数，则是介于0111和1000之 间。

物理加减法的行为正好和数轮的移动类似。只要所有的运算子和结果具有相同的位宽，那么有符号数或无符号数的形式就可用于相同的电路。比方说，设a、b和sum都是8位信号，表达式

1	sum = a+ b;

无论这些信号被转译成有符号数或无符号数，它都会引用相同的硬件且使用相同的二进制表示法。这种现象在其他算术运算中也是正确的（但是它不可用于非算术运算中，比方说有理数运算或溢出标志位的生成）。

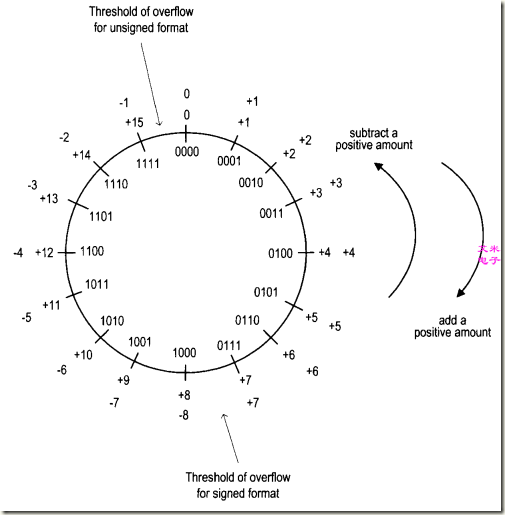
图1 4位二进制数轮

此外，当运算子或其结果的位宽不同时，我们需要区分它究竟使用哪一种符号类型。因为不同的符号类型需要不同的扩展位。对于无符号数，前置一个0，即 所谓的零扩展位；对于有符号数来说，需要前置n个所谓的符号扩展位。比方说4位二进制表示的-5为1011；当其扩展成8位时，应该变为 1111_1011，而不是0000_1011。

举个例子，设a和sum为8位信号，b为4位信号即b3b2b1b0。表达式

1	sum = a + b

需要将b扩展为8位。如果是无符号数形式，那么b扩展为0000_b3b2b1b0；如果是有符号数形式，那么b扩展为 b3b3b3b3_b3b2b1b0。上述表达式所引用的硬件包括位宽扩展电路和加法器。因为对于有符号数和无符号数来说，扩展电路是不同的；所以上面那 个表达式，对应有符号数和无符号数形式，要使用不同的硬件实现。

2 Verilog-1995中的有符号数

在Verilog-1995中，只有integer数据类型被转移成有符号数，而reg和wire数据类型则被转移成无符号数。由于integer 类型有固定的32位宽，因此它不太灵活。我们通常使用手动加上扩展位来实现有符号数运算。下面的代码片段将描述有符号数和无符号数的运算：

01	reg [7:0] a, b;

02	reg [3:0] c,

03	reg [7:0] sum1, sum2, sum3, sum4;

04

. . .

05	// same width. can be applied to signed and unsigned

06	sum1 = a + b;

07	// automatica 0 extension

08	sum2 = a + c;

09	// manual 0 extension

10	sum3 = a + {4{ 1'b0 }, c};

11	// manual sign extension

12	sum4 = a + {4{c[3]}, c};

在第一条语句中，a、b和sum1有相同的位宽，因此无论是转译成有符号数还是无符号数，它都将引用相同的加法器电路。

在第二条语句中，c的位宽仅为4，在加法运算中，它的位宽会被调整。因为reg类型被作为无符号数看待，所以c的前面会被自动置入0扩展位。

在第三条语句中，我们给c手动前置4个0，以实现和第二个表达式一样的效果。

在第四条语句中，我们需要把变量转译成有符号数。为了实现所需的行为，c必须扩展符号位到8位。没有其他的办法，只好手动扩展。在代码中，我们重复复制c的最高位4次（4{c[3]}）来创建具有扩展符号位的8位数。

3 Verilog-2001中的有符号数

在Verilog-2001中，有符号形式也被扩展到reg和wire数据类型中。哈哈，新加一个关键字，signed，可以按照下面的方式定义：

1	reg signed [7:0] a, b;

使用有符号数据类型， 第2节所述代码可以被改写为：

1	reg signed [7:0] a, b;

2	reg signed [3:0] c;

3	reg signed [7:0] sum1, sum4;

4

. . .

5	// same width. can be applied to signed and unsigned

6	sum1 = a + b;

7	// automatic sign extension

8	sum4 = a + c;

第一条语句将引用一个常规的加法器，因为a、b和sum1具有相同的位宽。

第二条语句，所有的右手边变量都具有signed数据类型，c被自动扩展符号位到8位。因此，无需再手动添加符号位。

在小型的数字系统中，我们通常可以选用有符号数或者无符号数。然而，在一些大型的系统中，会包括不同形式的子系统。Verilog是一种弱类型语 言，无符合变量和有符号变量可以在同一表达式中混用。根据Verilof的标准，只有当所有右手边的变量具有signed数据类型属性的时候，扩展符号位 才被执行。否则，所有的变量都只扩展0。考虑下面的代码片段：

1	reg signed [7:0] a, sum;

2	reg signed [3:0] b;

3	reg [3:0] c;

4

. . .

5	sum = a + b + c;

由于c不具有signed数据类型属性，因此右手边的变量b和c的扩展位为0。

Verilog有两个系统函数，$signed和$unsigned()，用以将括号内的表达式转换为signed和unsigned数据类型。比方说，我们可以转换c的数据类型，

1	sum = a + b + $signed(c);

现在，右手边的所有变量都具有signed数据类型属性，因此b和c将扩展符号位。

在复杂的表达式中，混用signed和unsigned数据类型将引入一些微妙的错误，因此应当避免混用。如果真的很有必要，那么表达式需要保持简单，同时通用转换函数，以确保数据类型的一致性。