Hello 2018 A,B,C,D

A. Modular Exponentiation

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

The following problem is well-known: given integers n and m, calculate

,

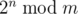where 2n = 2·2·...·2 (n factors), and 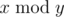 denotes the remainder of division of x by y.

You are asked to solve the "reverse" problem. Given integers n and m, calculate

.

Input

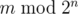The first line contains a single integer n (1 ≤ n ≤ 108).

The second line contains a single integer m (1 ≤ m ≤ 108).

Output

Output a single integer — the value of .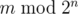

Examples

input

4
42

output

10

input

1
58

output

0

input

98765432
23456789

output

23456789

Note

In the first example, the remainder of division of 42 by 24 = 16 is equal to 10.

In the second example, 58 is divisible by 21 = 2 without remainder, and the answer is 0.

思路：

直接用题目讲的公式套

实现代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll mod(ll x,ll y){
    return x - (x/y)*y;
}
int main()
{
    int n;
    ll m;
    cin>>n>>m;
    cout<<mod(m,pow(,n))<<endl;
}

B. Christmas Spruce

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Consider a rooted tree. A rooted tree has one special vertex called the root. All edges are directed from the root. Vertex u is called a child of vertex v and vertex v is called a parent of vertex u if there exists a directed edge from v to u. A vertex is called a leaf if it doesn't have children and has a parent.

Let's call a rooted tree a spruce if its every non-leaf vertex has at least 3 leaf children. You are given a rooted tree, check whether it's a spruce.

The definition of a rooted tree can be found here.

Input

The first line contains one integer n — the number of vertices in the tree (3 ≤ n ≤ 1 000). Each of the next n - 1 lines contains one integer pi (1 ≤ i ≤ n - 1) — the index of the parent of the i + 1-th vertex (1 ≤ pi ≤ i).

Vertex 1 is the root. It's guaranteed that the root has at least 2 children.

Output

Print "Yes" if the tree is a spruce and "No" otherwise.

Examples

input

4
1
1
1

output

Yes

input

7
1
1
1
2
2
2

output

No

input

8
1
1
1
1
3
3
3

output

Yes

Note

The first example:

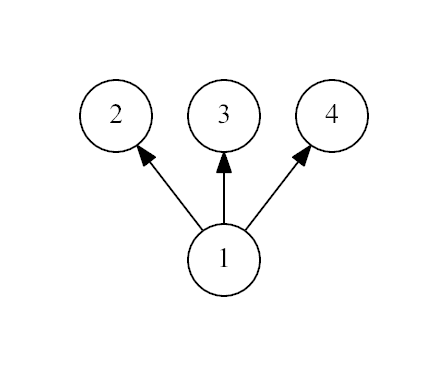
The second example:

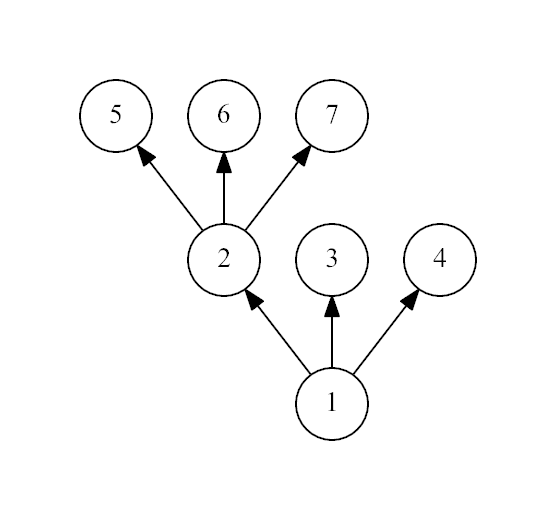
It is not a spruce, because the non-leaf vertex 1 has only 2 leaf children.

The third example:

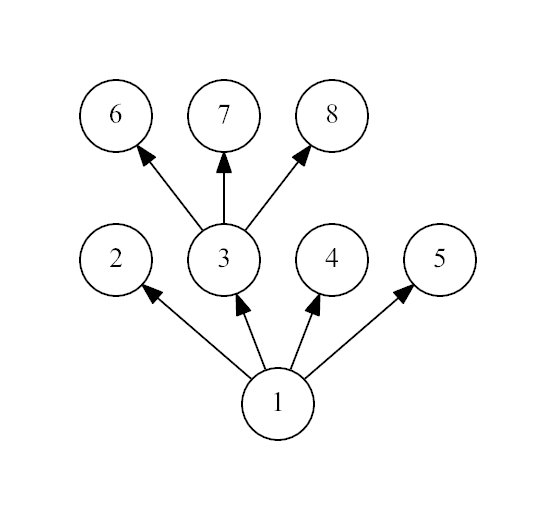
思路：

我是直接算出叶子节点的数量，再由这些叶子节点推出父节点的子节点数量，每个非叶子节点的父节点都要有3个以上的叶子节点。有个特殊判断就是没有叶子节点的除了叶子结点还有在中间的节点

这些节点的子节点全部为非叶子节点，要特判下。

实现代码：

#include<bits/stdc++.h>
using namespace std;
int a[],b[],c[];
int main()
{
    int n;
    cin>>n;
    for(int i = ;i <= n;i ++){
        cin>>a[i];
        b[a[i]]++;
    }
    for(int i = ;i <= n;i ++){
        if(b[i]==){
            c[a[i]]++;
        }
    }
    for(int i = ;i <= n;i ++){
        if(c[i]!=&&c[i]<){
            cout<<"No"<<endl; return ;
        }
        if(b[i]!=&&c[i]==){
            cout<<"No"<<endl; return ;
        }
    }
    cout<<"Yes"<<endl;
    return ;
}

C. Party Lemonade

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

A New Year party is not a New Year party without lemonade! As usual, you are expecting a lot of guests, and buying lemonade has already become a pleasant necessity.

Your favorite store sells lemonade in bottles of n different volumes at different costs. A single bottle of type i has volume 2i - 1 liters and costs ci roubles. The number of bottles of each type in the store can be considered infinite.

You want to buy at least L liters of lemonade. How many roubles do you have to spend?

Input

The first line contains two integers n and L (1 ≤ n ≤ 30; 1 ≤ L ≤ 109) — the number of types of bottles in the store and the required amount of lemonade in liters, respectively.

The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 109) — the costs of bottles of different types.

Output

Output a single integer — the smallest number of roubles you have to pay in order to buy at least L liters of lemonade.

Examples

input

4 12
20 30 70 90

output

150

input

4 3
10000 1000 100 10

output

10

input

4 3
10 100 1000 10000

output

30

input

5 787787787
123456789 234567890 345678901 456789012 987654321

output

44981600785557577

Note

In the first example you should buy one 8-liter bottle for 90 roubles and two 2-liter bottles for 30 roubles each. In total you'll get 12 liters of lemonade for just 150 roubles.

In the second example, even though you need only 3 liters, it's cheaper to buy a single 8-liter bottle for 10 roubles.

In the third example it's best to buy three 1-liter bottles for 10 roubles each, getting three liters for 30 roubles.

思路：

因为数据的特殊性（每个瓶子都是2^i-1)我们可以将L转换为2进制，逐位递推，因为相邻两个瓶子容量差距为1倍那么第i位花费最少的情况就是取a[i],a[i-1]*2中最小的，同时如果a[i]<a[i-1]那么肯定i-1位是优先选择a[i]，这样就求出了每一位最优的情况，那么当L转换为2进制的时候，如果位数上为1就优先取值，如果为0的话就要和前面的值判断下，如果当前位数的最优解小于之前的最优解那么直接覆盖掉之前的就行了因为i位的容量为2^i，大于前面所有容量之和，且花费更少那么肯定优先选i位代表的瓶子。

实现代码：

#include<bits/stdc++.h>
using namespace std;
#define ll unsigned long long

int main()
{
    ll n,m,a[];
    ll ans = ;
    cin>>n>>m;
    cin>>a[];
    for(int i = ;i < n; i++){
        cin>>a[i];
        a[i] = min(a[i],*a[i-]);
        a[i-] = min(a[i],a[i-]);
    }
    for(int i = n;i < ;i ++){
        a[i] = *a[i-];
    }
    for(int i = ;i < ;i ++){
        if(m & (<<i)) ans += a[i];
        ans = min(ans,a[i+]);
    }
    cout<<ans<<endl;
}

D. Too Easy Problems

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are preparing for an exam on scheduling theory. The exam will last for exactly T milliseconds and will consist of n problems. You can either solve problem i in exactly ti milliseconds or ignore it and spend no time. You don't need time to rest after solving a problem, either.

Unfortunately, your teacher considers some of the problems too easy for you. Thus, he assigned an integer ai to every problem i meaning that the problem i can bring you a point to the final score only in case you have solved no more than ai problems overall (including problem i).

Formally, suppose you solve problems p1, p2, ..., pk during the exam. Then, your final score s will be equal to the number of values of jbetween 1 and k such that k ≤ apj.

You have guessed that the real first problem of the exam is already in front of you. Therefore, you want to choose a set of problems to solve during the exam maximizing your final score in advance. Don't forget that the exam is limited in time, and you must have enough time to solve all chosen problems. If there exist different sets of problems leading to the maximum final score, any of them will do.

Input

The first line contains two integers n and T (1 ≤ n ≤ 2·105; 1 ≤ T ≤ 109) — the number of problems in the exam and the length of the exam in milliseconds, respectively.

Each of the next n lines contains two integers ai and ti (1 ≤ ai ≤ n; 1 ≤ ti ≤ 104). The problems are numbered from 1 to n.

Output

In the first line, output a single integer s — your maximum possible final score.

In the second line, output a single integer k (0 ≤ k ≤ n) — the number of problems you should solve.

In the third line, output k distinct integers p1, p2, ..., pk (1 ≤ pi ≤ n) — the indexes of problems you should solve, in any order.

If there are several optimal sets of problems, you may output any of them.

Examples

input

5 300
3 100
4 150
4 80
2 90
2 300

output

2
3
3 1 4

input

2 100
1 787
2 788

output

0
0

input

2 100
2 42
2 58

output

2
2
1 2

Note

In the first example, you should solve problems 3, 1, and 4. In this case you'll spend 80 + 100 + 90 = 270 milliseconds, falling within the length of the exam, 300 milliseconds (and even leaving yourself 30 milliseconds to have a rest). Problems 3 and 1 will bring you a point each, while problem 4 won't. You'll score two points.

In the second example, the length of the exam is catastrophically not enough to solve even a single problem.

In the third example, you have just enough time to solve both problems in 42 + 58 = 100 milliseconds and hand your solutions to the teacher with a smile.

思路：

题目意思有点难懂，看了半天，给出 n m,一个代表题目数量，一个代表做题耗时加起来不得超过m，n组数据，每组有两个数 ,ai 和 ti，ti为耗时，ai不得小于已选题目的数量，如第一个样例中4不合格因为a4 = 2，而包括a4的时候一共选了3道题，所以a4不符合要求，这道题用优先队列来写的话会很方便，自定义个优先队列，ai为第一优先级，ti为第二优先级，ai小的优先，如果相同则ti大的优先，判断ai是否符合大于所选问题总数，队列中的ti之和是否小于等于规定的时间t，如果不符合要求就释放队首，再添加下一个问题进行判断，这样不断判下来，最后得到的就是符合要求的。

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{
    int x,y,id;
}a[];
struct cmp1{
    bool operator()(const node &c,const node &d){
        if(c.x!=d.x)return c.x>d.x;return c.y<d.y;
    }
};
bool cmp2(node c,node d){
    return c.y < d.y;
}
priority_queue<node, vector<node>, cmp1>q;
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = ;i < n;i ++){
      cin>>a[i].x>>a[i].y;
      a[i].id = i + ;
    }
    sort(a,a+n,cmp2);
    int m1 = m;
    int ans = ;
    for(int i = ;i < n; i++){
      if(m1 < a[i].y)  break;
      if(ans < a[i].x){
      m1 -= a[i].y;
      q.push(a[i]);
      ans ++;
      }
      while(!q.empty()&&q.top().x<ans){
        ans --;
        m1 += q.top().y;
        q.pop();
      }
    }
    cout<<ans<<endl<<ans<<endl;
    while(!q.empty()){
        cout<<q.top().id<<" ";
        q.pop();
    }
    cout<<endl;
}