图论之最小生成树之Kruskal算法

Kruskal算法，又称作为加边法，是配合并查集实现的。

图示：

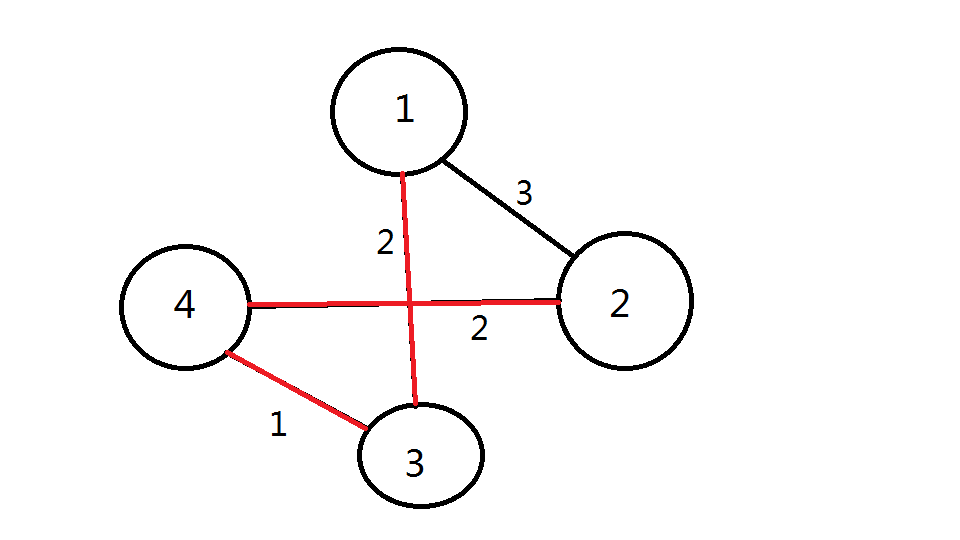
如图，这是一个带权值无向图我们要求它的最小生成树。

---

首先，我们发现在1的所有边上，连到3的边的边权值最小，所以加上这条边。

---

然后在3上，连到4的边权值最小，加上这条边。

---

最后，4连到2的边是最小的，加上这条边。

现在，所有点都连通了，所以这个图的最小生成树就是2+2+1=5

---

从上述操作中可以看出，Kruskal算法是需要贪心的思想的。

那怎么来实现这个贪心呢？

简单，一个sort足矣！

---

所以这整个Kruskal算法的思路是：

1. 初始化
2. 排序
3. for循环遍历所有边，如果两个图没有连通（get(x)!=get(y)）,就给它加上边，cnt再加上这条边的边权值。

例题及讲解

END